题目内容
已知△ABC∽△DEF，若△ABC与△DEF的相似比为3：4，则△ABC与△DEF的面积比为 ．
考点：相似三角形的性质
专题：
分析：由△ABC∽△DEF，若△ABC与△DEF的相似比为3：4，根据相似三角形的面积比等于相似比的平方，即可求得答案．
解答：解：∵△ABC∽△DEF，△ABC与△DEF的相似比为3：4，
∴△ABC与△DEF的面积比为9：16．
故答案为：9：16．
∴△ABC与△DEF的面积比为9：16．
故答案为：9：16．
点评：此题考查了相似三角形的性质．此题比较简单，注意熟记定理是解此题的关键．
练习册系列答案
相关题目
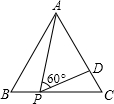如图，如图，等边△ABC的边长为3，P为BC上一点，且BP=1，D为AC上一点，若∠APD=60°，则CD的长是（ ）A、
| ||
B、
| ||
C、
| ||
D、
|
在边长为1的小正方形网格中（如图），△AOB的顶点均在格点上一个几何体的三视图如图所示．后视图为中心对称的一项是（ ）
A、 |
B、 |
C、 |
D、 |
铁丝AB=12米，AD=13米，AC=15米，又测得地面上B，C两点之间距离是9米，B，D两点之间距离5米，则电线杆和地面是否垂直，为什么？已知二次函数y=ax2+bx+c的图象过点A（1，2），B（3，2），C（5，7）．若点M（-2，y1），N（-1，y2），也在该二次函数y=ax2+bx+c的图象上，则下列结论正确的是（ ）
| A、y1=y2 |
| B、y1＜y2 |
| C、y1＞y2 |
| D、y1≤y2 |