题目内容
11.对于反比例函数y=$\frac{{k}^{2}}{x}$(k≠0),下列说法不正确的是( )| A. | 它的图象分布在第一、三象限 | B. | 点(k,k)在它的图象上 | ||
| C. | 它的图象关于原点对称 | D. | 在每个象限内y随x的增大而增大 |
分析 利用反比例函数的性质用排除法解答.
解答 解:A、反比例函数y=$\frac{{k}^{2}}{x}$(k≠0),因为k2>0,根据反比例函数的性质它的图象分布在第一、三象限,故本选项错误;
B、把点(k,k),代入反比例函数y=$\frac{{k}^{2}}{x}$(k≠0)中成立,故本选项错误;
C、反比例函数y=$\frac{{k}^{2}}{x}$(k≠0),k2>0根据反比例函数的性质它的图象分布在第一、三象限,是关于原点对称,故本选项错误;
D、反比例函数y=$\frac{{k}^{2}}{x}$(k≠0),因为k2>0,根据反比例函数的性质它的图象分布在第一、三象限,在每个象限内,y随x的增大而减小,故本选项正确.
故选:D.
点评 本题考查了反比例函数的性质:①、当k>0时,图象分别位于第一、三象限;当k<0时,图象分别位于第二、四象限.
②、当k>0时,在同一个象限内,y随x的增大而减小;当k<0时,在同一个象限,y随x的增大而增大.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 已知:如图,E,F是?ABCD的对角线AC上的两点,BE∥DF,求证:AF=CE.
已知:如图,E,F是?ABCD的对角线AC上的两点,BE∥DF,求证:AF=CE.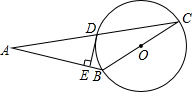 如图,在△ABC中,AB=BC,以BC为直径的⊙O与AC交于点D,DE⊥AB于点E.
如图,在△ABC中,AB=BC,以BC为直径的⊙O与AC交于点D,DE⊥AB于点E.