题目内容
3.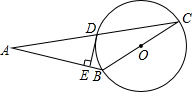 如图,在△ABC中,AB=BC,以BC为直径的⊙O与AC交于点D,DE⊥AB于点E.
如图,在△ABC中,AB=BC,以BC为直径的⊙O与AC交于点D,DE⊥AB于点E.(1)求证:DE是⊙O的切线.
(2)若sinA=$\frac{1}{3}$,DE=$\sqrt{2}$,求⊙O的直径.
分析 (1)连接OD,根据等腰三角形的性质和平行线的判定定理得到OD∥AB,根据垂直的定义和平行线的性质得到∠DEA=90°,根据切线的判定定理证明即可;
(2)连接BD,根据相似三角形的性质列出比例式,计算即可.
解答 (1)证明:连接OD,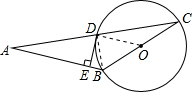
∵OD=OC,
∴∠C=∠ODC,
∵AB=BC,
∴∠A=∠C,
∴∠ODC=∠A,
∴OD∥AB,
∴∠ODE=∠DEA;
∵DE⊥AB,
∴∠DEA=90°,
∴∠ODE=90°,即DE⊥OD,
∴DE是⊙O的切线;
(2)连接BD,
∵BC为⊙O的直径,
∴BD⊥AC,又DE⊥AB,
∴AD2=AE•AB,
∵sinA=$\frac{1}{3}$,DE=$\sqrt{2}$,
∴AD=3$\sqrt{2}$,AE=4,
∴(3$\sqrt{2}$)2=4×AB,
解得,AB=$\frac{9}{2}$,
∴BC=$\frac{9}{2}$,
即⊙O的直径为$\frac{9}{2}$.
点评 本题考查的是切线的判定,掌握切线的判定定理:经过半径的外端且垂直于这条半径的直线是圆的切线是解题的关键.

练习册系列答案
相关题目
11.对于反比例函数y=$\frac{{k}^{2}}{x}$(k≠0),下列说法不正确的是( )
| A. | 它的图象分布在第一、三象限 | B. | 点(k,k)在它的图象上 | ||
| C. | 它的图象关于原点对称 | D. | 在每个象限内y随x的增大而增大 |
8.某汽车销售公司计划销售A、B两种型号的汽车共80辆,该公司所筹资金不少于660万元,但不超过672万元,且所筹资金全部用于购进新车,设A型汽车购进x辆,该公司销售A、B两种汽车获得利润y(万元),两种汽车的成本和售价如表:
(1)该公司对这两种汽车进货有哪几种方案?
(2)列出y关于x的函数关系式,并通过函数的性质判断如何进货该公司获得利润最大?
(3)根据市场调查,每辆B型汽车售价不会改变,每辆A型汽车的售价将会提高a万元(a>0),且所进的两种汽车可全部售出,该公司又将如何进货获得利润最大?(注:利润=售价-成本)
| A | B | |
| 成本(万元/辆) | 6 | 12 |
| 售价(万元/辆) | 9 | 16 |
(2)列出y关于x的函数关系式,并通过函数的性质判断如何进货该公司获得利润最大?
(3)根据市场调查,每辆B型汽车售价不会改变,每辆A型汽车的售价将会提高a万元(a>0),且所进的两种汽车可全部售出,该公司又将如何进货获得利润最大?(注:利润=售价-成本)
 如图,已知DE∥BC,∠1=∠2,求证:∠B=∠C.
如图,已知DE∥BC,∠1=∠2,求证:∠B=∠C.