题目内容
9．如果三角形ABC中，∠A：∠B：∠C=1：1：2，那么BC：AC：AB的值为（ ）| A． | 1：1：2 | B． | 1：2：1 | C． | 2：1：1 | D． | 1：1：$\sqrt{2}$ |
分析 先根据三角形内角和判断出△ABC的形状，再根据直角三角形的性质解答即可．
解答 解：因为∠A：∠B：∠C=1：1：2，∠A+∠B+∠C=180°，
可得：△ABC是等腰直角三角形，
可得：BC：AC：AB=1：1：$\sqrt{2}$，
故选：D．
点评 本题考查的是等腰直角三角形的性质，即如果∠A：∠B：∠C=1：1：2，那么这个三角形就是等腰直角三角形．
练习册系列答案
优学名师名题系列答案
相关题目
如图，已知△ABC是等边三角形，BE=CD，EH⊥AD于H，DG∥EH交CE于G，求证：EG=2HD．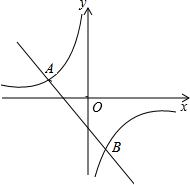
如图，一次函数y1的图象与反比例函数y2的图象交于A（-5，2）、B（m，-5）两点．
18．若分式$\frac{|x|-1}{x+1}$的值为0，则（ ）
| A． | x=±1 | B． | x=1 | C． | x=-1 | D． | x=0 |