题目内容
1.将一个半径为4cm,圆心角为270°的扇形围成一个圆锥的侧面(拼接处不重叠),则该圆锥的高为$\sqrt{7}$cm.分析 设圆锥的底面圆的半径为r,根据圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长和弧长公式得到2πr=$\frac{270•π•4}{180}$,解得r=3,然后利用勾股定理计算圆锥的高.
解答 解:设圆锥的底面圆的半径为r,
根据题意得2πr=$\frac{270•π•4}{180}$,
解得:r=3,
该圆锥的高为:$\sqrt{{4}^{2}-{3}^{2}}$=$\sqrt{7}$.
故答案为:$\sqrt{7}$.
点评 本题考查了圆锥的计算:圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长.

练习册系列答案
相关题目
11.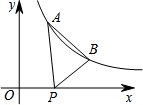 如图所示,已知A($\frac{1}{2}$,y1),B(2,y2)为反比例函数y=$\frac{1}{x}$图象上的两点,动点P在x轴的非负半轴上运动,当线段AP与线段BP之差达到最大值时,点P的坐标是( )
如图所示,已知A($\frac{1}{2}$,y1),B(2,y2)为反比例函数y=$\frac{1}{x}$图象上的两点,动点P在x轴的非负半轴上运动,当线段AP与线段BP之差达到最大值时,点P的坐标是( )
 如图所示,已知A($\frac{1}{2}$,y1),B(2,y2)为反比例函数y=$\frac{1}{x}$图象上的两点,动点P在x轴的非负半轴上运动,当线段AP与线段BP之差达到最大值时,点P的坐标是( )
如图所示,已知A($\frac{1}{2}$,y1),B(2,y2)为反比例函数y=$\frac{1}{x}$图象上的两点,动点P在x轴的非负半轴上运动,当线段AP与线段BP之差达到最大值时,点P的坐标是( )| A. | $({\frac{5}{2},0})$ | B. | (3,0) | C. | $({\frac{7}{2},0})$ | D. | (4,0) |
12.七(1)班学雷锋小组整理校实验室,已知6个人共要做4小时完成,则每人每小时的工作效率是( )
| A. | $\frac{2}{3}$ | B. | $\frac{3}{2}$ | C. | $\frac{1}{12}$ | D. | $\frac{1}{24}$ |
9.如果三角形ABC中,∠A:∠B:∠C=1:1:2,那么BC:AC:AB的值为( )
| A. | 1:1:2 | B. | 1:2:1 | C. | 2:1:1 | D. | 1:1:$\sqrt{2}$ |
16.下列计算正确的是( )
| A. | 5m-2m=3 | B. | 2a•3a=6a | C. | (ab3)2=ab6 | D. | 2m3n÷(mn)=2m2 |
10.下面的计算正确的是( )
| A. | a+2a=3a2 | B. | a3÷a=3 | C. | a2•a3=a5 | D. | -(a)3=a3 |