题目内容
13.计算:(x-1+y-1)÷(x-2-y-2)分析 首先应用平方差公式,可得(x-2-y-2)=(x-1+y-1)(x-1-y-1),据此推得(x-1+y-1)÷(x-2-y-2)=$\frac{1}{{x}^{-1}{-y}^{-1}}$;然后根据负整数指数幂的运算方法,求出算式的值是多少即可.
解答 解:(x-1+y-1)÷(x-2-y-2)
=(x-1+y-1)÷[(x-1+y-1)(x-1-y-1)]
=$\frac{1}{{x}^{-1}{-y}^{-1}}$
=$\frac{1}{\frac{1}{x}-\frac{1}{y}}$
=$\frac{xy}{y-x}$
点评 此题主要考查了负整数指数幂的运算,要熟练掌握,解答此题的关键是要明确:①a-p=$\frac{1}{{a}^{p}}$(a≠0,p为正整数);②计算负整数指数幂时,一定要根据负整数指数幂的意义计算;③当底数是分数时,只要把分子、分母颠倒,负指数就可变为正指数.

练习册系列答案
 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
3.下表中的字母都是按移动规律排列的.
我们把某格中的字母的和所得多项式称为特征多项式,例如第1格的“特征多项式”为6x+2y,第2格的“特征多项式”为9x+4y,回答下列问题.
(1)第3格的“特征多项式”为12x+6y,第4格的“特征多项式”为15x+8y,第n格的“特征多项式”为3(n+1)x+2ny(n为正整数);
(2)求第6格的“特征多项式”与第5格的“特征多项式”的差.
| 序号 | 1 | 2 | 3 | … |
图形 | x x y x x y x x | x x x y y x x x y y x x x | x x x x y y y x x x x y y y x x x x | … |
(1)第3格的“特征多项式”为12x+6y,第4格的“特征多项式”为15x+8y,第n格的“特征多项式”为3(n+1)x+2ny(n为正整数);
(2)求第6格的“特征多项式”与第5格的“特征多项式”的差.
2.下列每一组数据中的三个数值分别为三角形的三边长,能构成直角三角形的是( )
| A. | 3、4、5 | B. | 7、8、9 | C. | 1、2、3 | D. | 6、12、13 |
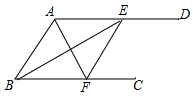 如图,AD∥BC,AF平分∠BAD交BC于点F,BE平分∠ABC交AD于点E.求证:
如图,AD∥BC,AF平分∠BAD交BC于点F,BE平分∠ABC交AD于点E.求证: 如图,在△ABC中,已知AD是BC边上的高,DC=1,BD=2,tanB=cos∠DAC,则AB的值为$\sqrt{7}$.
如图,在△ABC中,已知AD是BC边上的高,DC=1,BD=2,tanB=cos∠DAC,则AB的值为$\sqrt{7}$.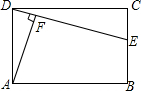 如图所示,在矩形ABCD中,E是BC上一点,AF⊥DE于点F.
如图所示,在矩形ABCD中,E是BC上一点,AF⊥DE于点F.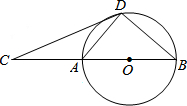 如图,D为⊙O上一点,点C在直径BA的延长线上,∠CDA=∠CBD.
如图,D为⊙O上一点,点C在直径BA的延长线上,∠CDA=∠CBD.