题目内容
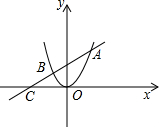 已知:如图,抛物线y=ax2与直线y=x+b交于A、B两点,若A点的坐标为(1,2).求:
已知:如图,抛物线y=ax2与直线y=x+b交于A、B两点,若A点的坐标为(1,2).求:(1)抛物线与直线的解析式;
(2)B点的坐标;
(3)△AOB的面积.
考点:待定系数法求二次函数解析式,待定系数法求一次函数解析式,二次函数的性质
专题:
分析:(1)将A点的坐标代入y=x+b中,可求直线的解析式,将A点坐标代入y=ax2中,可求抛物线的解析式.
(2)联立方程,解方程组即可求得B的坐标;
(3)根据△AOC的面积=△AOC的面积-△BOC的面积,即可求得.
(2)联立方程,解方程组即可求得B的坐标;
(3)根据△AOC的面积=△AOC的面积-△BOC的面积,即可求得.
解答:解:(1)∵直线y=x+b过点A(1,2),
∴2=1+b,
解得b=1,
∴直线AB所表示的函数解析式为y=x+1,
∵抛物线y=ax2过点A(1,2),
∴a×12=2,
解得a=2,
∴抛物线所表示的函数解析式为y=2x2.
(2)解
,得
或
,
∴B的坐标为(-
,
).
(3)由直线AB所表示的函数解析式为y=x+1,
可知直线与x轴的交点C的坐标为(-1,0),
∵△AOC的面积=
×1×2=1,△BOC的面积=
×1×
=
,
∴△AOB的面积=1-
=
.
∴2=1+b,
解得b=1,
∴直线AB所表示的函数解析式为y=x+1,
∵抛物线y=ax2过点A(1,2),
∴a×12=2,
解得a=2,
∴抛物线所表示的函数解析式为y=2x2.
(2)解
|
|
|
∴B的坐标为(-
| 1 |
| 2 |
| 1 |
| 2 |
(3)由直线AB所表示的函数解析式为y=x+1,
可知直线与x轴的交点C的坐标为(-1,0),
∵△AOC的面积=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
∴△AOB的面积=1-
| 1 |
| 4 |
| 3 |
| 4 |
点评:本题考查了一次函数、二次函数解析式的求法,以及直线和抛物线的交点,与坐标轴的交点等,属于基础知识,需熟练掌握.

练习册系列答案
相关题目
一元二次方程(x-1)(x-2)=0的两根和是( )
| A、2 | B、-2 | C、3 | D、-3 |