题目内容
阅读下面材料:
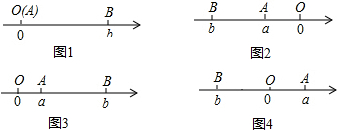
点A、B在数轴上分别表示实数a、b,A、B两点之间的距离表示为|AB|.
当A、B两点中有一点在原点时,不妨设点A在原点,
如图1,|AB|=|OB|=|b|=|a-b|;
当A、B两点都不在原点时,
如图2,点A、B都在原点的右边
|AB|=|OB|-|OA|=|b|-|a|=b-a=|a-b|;
如图3,点A、B都在原点的左边,
|AB|=|OB|-|OA|=|b|-|a|=-b-(-a)=|a-b|;
如图4,点A、B在原点的两边,
|AB|=|OB|+|OA|=|a|+|b|=a+(-b)=|a-b|;
回答下列问题:
①数轴上表示2和5的两点之间的距离是 ,数轴上表示-2和-5的两点之间的距离是 ,数轴上表示1和-3的两点之间的距离是 ;
②数轴上表示x和-1的两点A和B之间的距离是 ,如果|AB|=2,那么x为 ;
③当代数式|x+1|+|x-2|+|x+3|取最小值时,相应的x的值是 ;此时代数式|x+1|+|x-2|+|x+3|的值是 .
点A、B在数轴上分别表示实数a、b,A、B两点之间的距离表示为|AB|.
当A、B两点中有一点在原点时,不妨设点A在原点,
如图1,|AB|=|OB|=|b|=|a-b|;
当A、B两点都不在原点时,
如图2,点A、B都在原点的右边
|AB|=|OB|-|OA|=|b|-|a|=b-a=|a-b|;
如图3,点A、B都在原点的左边,
|AB|=|OB|-|OA|=|b|-|a|=-b-(-a)=|a-b|;
如图4,点A、B在原点的两边,
|AB|=|OB|+|OA|=|a|+|b|=a+(-b)=|a-b|;

回答下列问题:
①数轴上表示2和5的两点之间的距离是
②数轴上表示x和-1的两点A和B之间的距离是
③当代数式|x+1|+|x-2|+|x+3|取最小值时,相应的x的值是
考点:绝对值,数轴
专题:
分析:①直接利用数轴分别求出两点之间的距离;
②利用已知条件分析得出A和B之间的距离以及x的值;
③利用当x取到-1,2,-3的中间数字时,此代数式最小,进而得出答案.
②利用已知条件分析得出A和B之间的距离以及x的值;
③利用当x取到-1,2,-3的中间数字时,此代数式最小,进而得出答案.
解答:解:①数轴上表示2和5的两点之间的距离是:5-2=3;
数轴上表示-2和-5的两点之间的距离是:-2-(-5)=3;
数轴上表示1和-3的两点之间的距离是:1-(-3)=4;
故答案为:3,3,4;
②数轴上表示x和-1的两点A和B之间的距离是:|x+1|,
如果|AB|=2,那么x为-3或1;
故答案为:|x+1|,-3或1;
③当代数式|x+1|+|x-2|+|x+3|取最小值时,相应的x的值是:1;
此时代数式|x+1|+|x-2|+|x+3|的值是5.
故答案为:1,5.
数轴上表示-2和-5的两点之间的距离是:-2-(-5)=3;
数轴上表示1和-3的两点之间的距离是:1-(-3)=4;
故答案为:3,3,4;
②数轴上表示x和-1的两点A和B之间的距离是:|x+1|,
如果|AB|=2,那么x为-3或1;
故答案为:|x+1|,-3或1;
③当代数式|x+1|+|x-2|+|x+3|取最小值时,相应的x的值是:1;
此时代数式|x+1|+|x-2|+|x+3|的值是5.
故答案为:1,5.
点评:此题主要考查了绝对值,利用数轴得出代数式最小值是解题关键.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案 应用题作业本系列答案
应用题作业本系列答案
相关题目
下列叙述中,不正确的是( )
| A、射线AB与射线BA是不同的两条射线 |
| B、两点之间,线段最短 |
| C、两点确定一条直线 |
| D、锐角和钝角互补 |
抛物线y=-4(x-8)2-3的顶点坐标是( )
| A、(8,3) |
| B、(8,-3) |
| C、(-8,3) |
| D、(-8,-3) |
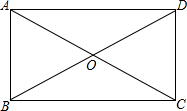 如图,在矩形ABCD中,对角线AC、BD交于点O,已知∠AOD=120°,AB=4,则AC的长为
如图,在矩形ABCD中,对角线AC、BD交于点O,已知∠AOD=120°,AB=4,则AC的长为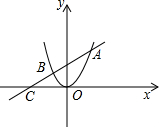 已知:如图,抛物线y=ax2与直线y=x+b交于A、B两点,若A点的坐标为(1,2).求:
已知:如图,抛物线y=ax2与直线y=x+b交于A、B两点,若A点的坐标为(1,2).求: