题目内容
2. 如图,在△ABC中,BD平分∠ABC,
如图,在△ABC中,BD平分∠ABC,(1)作图:作BC边的垂直平分线分别交BC,BD于点E,F(用尺规作图法,保留作图痕迹,不要求写作法);
(2)在(1)的条件下,连结CF,若∠A=60°,∠ABD=24°,求∠ACF的度数.
分析 (1)分别以B、C为圆心,大于$\frac{1}{2}$BC长为半径画弧,两弧交于两点,过两点画直线,与BC,BD的交点记作E,F;
(2)根据角平分线性质可得∠ABC=2∠ABD,∠ABD=∠CBD,然后利用三角形内角和定理可得∠ACB的度数,根据线段垂直平分线的性质可得BF=CF,进而可得∠FCB=∠FBC=24°,再根据角的和差关系可得答案.
解答 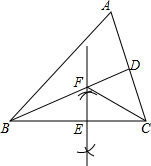 解:(1)如图所示:
解:(1)如图所示:
(2)∵BD平分∠ABC,
∴∠ABC=2∠ABD,∠ABD=∠CBD,
∵∠ABD=24°,
∴∠ABC=48°,∠DBC=24°,
∵∠A=60°,
∴∠ACB=180°-60°-48°=72°,
∵EF是BC的垂直平分线,
∴BF=CF,
∴∠FCB=∠FBC=24°,
∴∠ACF=72°-24°=48°.
点评 此题主要考查了复杂作图,以及线段垂直平分线的性质,三角形内角和定理,角平分线的性质,关键是掌握线段垂直平分线上任意一点,到线段两端点的距离相等.

练习册系列答案
 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案
相关题目
14.已知两圆的半径分别为一元二次方程x2-7x+12=0的二根,圆心距为1,则两圆位置关系为( )
| A. | 内切 | B. | 外切 | C. | 相交 | D. | 相离 |
 如图,有一块长和宽分别为70厘米和50厘米的长方形铁皮,要在它的四角截去四个全等的小正方形,做成一个无盖的长方体铁盒,且使盒子的底面积为1500平方厘米,那么做成盒子的高是多少厘米?
如图,有一块长和宽分别为70厘米和50厘米的长方形铁皮,要在它的四角截去四个全等的小正方形,做成一个无盖的长方体铁盒,且使盒子的底面积为1500平方厘米,那么做成盒子的高是多少厘米? 如图,两条互相平行的河岸,在河岸一边测得AB为20米,在另一边测得CD为70米,用测角器测得∠ACD=30°,测得∠BDC=45°,求两条河岸之间的距离.($\sqrt{2}≈1.4,\sqrt{3}$≈1.7,结果保留整数)
如图,两条互相平行的河岸,在河岸一边测得AB为20米,在另一边测得CD为70米,用测角器测得∠ACD=30°,测得∠BDC=45°,求两条河岸之间的距离.($\sqrt{2}≈1.4,\sqrt{3}$≈1.7,结果保留整数)