题目内容
17. 如图,两条互相平行的河岸,在河岸一边测得AB为20米,在另一边测得CD为70米,用测角器测得∠ACD=30°,测得∠BDC=45°,求两条河岸之间的距离.($\sqrt{2}≈1.4,\sqrt{3}$≈1.7,结果保留整数)
如图,两条互相平行的河岸,在河岸一边测得AB为20米,在另一边测得CD为70米,用测角器测得∠ACD=30°,测得∠BDC=45°,求两条河岸之间的距离.($\sqrt{2}≈1.4,\sqrt{3}$≈1.7,结果保留整数)
分析 分别过点A、B作CD的垂线交CD于点E、F,令两条河岸之间的距离为h.则AE=BF=h,EF=AB=20.解Rt△ACE,得出CE=$\sqrt{3}$h,解Rt△BDF,求出DF=BF=h,根据CD=CE+EF+FD=70列出方程,求解即可.
解答 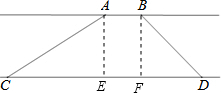 解:如图,分别过点A、B作CD的垂线交CD于点E、F,令两条河岸之间的距离为h.
解:如图,分别过点A、B作CD的垂线交CD于点E、F,令两条河岸之间的距离为h.
∵AE⊥CD,BF⊥CD,AB∥CD,AB=20,
∴AE=BF=h,EF=AB=20.
在Rt△ACE中,∵∠AEC=90°,∠ACE=30°,
∴tan∠ACE=$\frac{AE}{CE}$,即tan30°=$\frac{h}{CE}$,
∴CE=$\sqrt{3}$h.
在Rt△BDF中,∵∠BFD=90°,∠BDF=45°,
∴DF=BF=h.
∵CD=70,
∴CE+EF+FD=70,
∴$\sqrt{3}$h+20+h=70,
∴h=25($\sqrt{3}$-1)≈18.
答:两条河岸之间的距离约为18米.
点评 本题考查了解直角三角形的应用,通过作辅助线构造直角三角形,用含h的代数式分别表示出CE与FD是解题的关键.

练习册系列答案
 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目
8. 如图,在⊙O中,半径OA⊥弦BC,∠AOB=50°,点D在圆上,则∠ADC的度数是( )
如图,在⊙O中,半径OA⊥弦BC,∠AOB=50°,点D在圆上,则∠ADC的度数是( )
 如图,在⊙O中,半径OA⊥弦BC,∠AOB=50°,点D在圆上,则∠ADC的度数是( )
如图,在⊙O中,半径OA⊥弦BC,∠AOB=50°,点D在圆上,则∠ADC的度数是( )| A. | 50° | B. | 40° | C. | 30° | D. | 25° |
6.下列代数式中,单项式是( )
| A. | a-b | B. | -3a | C. | $\frac{a+b}{3}$ | D. | $\frac{b}{a}$ |
 如图,在Rt△ABC中,∠C=90°,线段AB的垂直平分线交AB于点D,交BC于点E,若AC=4,CE=3,求BE的长.
如图,在Rt△ABC中,∠C=90°,线段AB的垂直平分线交AB于点D,交BC于点E,若AC=4,CE=3,求BE的长. 如图,在△ABC中,BD平分∠ABC,
如图,在△ABC中,BD平分∠ABC,