题目内容
8.设a,b是整数,方程x2+ax+b=0的一个根是$\sqrt{4-2\sqrt{3}}$,则$\frac{{a}^{2}+{b}^{2}}{ab}$的值为-2.分析 方程的一个根是x=$\sqrt{4-2\sqrt{3}}$,代入方程,由a,b是整数,列出关于a,b的方程组,解方程组即可求出a、b的值,进而即可求出代数式的值.
解答 解:把x=$\sqrt{4-2\sqrt{3}}$代入方程有:
($\sqrt{4-2\sqrt{3}}$)2+a($\sqrt{3-2\sqrt{3}+1}$)+b=0,
4-2$\sqrt{3}$+($\sqrt{3}$-1)a+b=(a-2)$\sqrt{3}$+4-a+b=0.
∵a,b是整数,
∴$\left\{\begin{array}{l}{a-2=0}\\{4-a+b=0}\end{array}\right.$,解得:$\left\{\begin{array}{l}{a=2}\\{b=-2}\end{array}\right.$,
∴$\frac{{a}^{2}+{b}^{2}}{ab}$=$\frac{{2}^{2}+(-2)^{2}}{2×(-2)}$=-2.
故答案为:-2.
点评 本题考查的是一元二次方程的解,把方程的解代入方程,根据二次根式的性质化简,得到关于a,b的方程组,求出a,b的值,即可求解.

练习册系列答案
 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案
相关题目
9.两个锐角分别相等的两个直角三角形( )全等.
| A. | 不一定 | B. | 一定不 | C. | 一定 | D. | 以上都不对 |
 如图,CD分别交AD,EG于点D,G,EB分别交AD,EG于点A,E,AC交EG于点F,FH交AD于点H,AD平分∠BAC,EG∥AD,CG⊥EG,∠C=∠AFH.
如图,CD分别交AD,EG于点D,G,EB分别交AD,EG于点A,E,AC交EG于点F,FH交AD于点H,AD平分∠BAC,EG∥AD,CG⊥EG,∠C=∠AFH. 已知,如图,在△ABC中,OB和OC分别平分∠ABC和∠ACB,过O作DE∥BC,分别交AB、AC于点D、E,若BD+CE=5,则线段DE的长为5.
已知,如图,在△ABC中,OB和OC分别平分∠ABC和∠ACB,过O作DE∥BC,分别交AB、AC于点D、E,若BD+CE=5,则线段DE的长为5.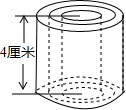 如图所示,圆柱的高是4厘米,当圆柱底面半径r(cm)变化时,圆柱的体积V(cm3)也随之变化.
如图所示,圆柱的高是4厘米,当圆柱底面半径r(cm)变化时,圆柱的体积V(cm3)也随之变化. 设二次函数y=ax2+bx+c(a≠0)图象如图所示,经过点(-1,0),试判断a、b、c、a+b+c、a-b+c、b2-4ac的符号.
设二次函数y=ax2+bx+c(a≠0)图象如图所示,经过点(-1,0),试判断a、b、c、a+b+c、a-b+c、b2-4ac的符号.