题目内容
3.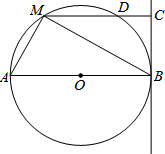 如图,直线BC与半径为6的⊙O相切于点B,点M是圆上的动点,过点M作MC⊥BC,垂足为C,MC与⊙O交于点D,AB为⊙O的直径,连接MA、MB,设MC的长为x,(6<x<12).
如图,直线BC与半径为6的⊙O相切于点B,点M是圆上的动点,过点M作MC⊥BC,垂足为C,MC与⊙O交于点D,AB为⊙O的直径,连接MA、MB,设MC的长为x,(6<x<12).(1)当x=9时,求BM的长和△ABM的面积;
(2)是否存在点M,使MD•DC=20?若存在,请求出x的值;若不存在,请说明理由.
分析 (1)利用切线的性质以及平行线的性质进而得出∠BMC=∠ABM以及∠BCM=∠AMB=90°,即可得出△BCM∽△AMB,根据相似三角形的性质即可求得BM的长,根据勾股定理求得BC,然后根据三角形面积公式求得△ABM的面积;
(2)首先得出四边形OBCE为矩形,进而得出MD•DC=2(x-6)•(12-x),进而求出最值即可判定.
解答 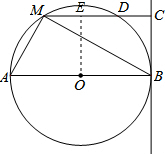 (1)证明:∵直线BC与半径为6的⊙O相切于点B,且AB为⊙O的直径,
(1)证明:∵直线BC与半径为6的⊙O相切于点B,且AB为⊙O的直径,
∴AB⊥BC,
又∵MC⊥BC,
∴AB∥MC,
∴∠BMC=∠ABM,
∵AB是⊙O的直径,
∴∠AMB=90°,
∴∠BCM=∠AMB=90°,
∴△BCM∽△AMB,
∴$\frac{BM}{AB}$=$\frac{MC}{BM}$,
∴BM2=AB•MC=12×9=108,
∴BM=6$\sqrt{3}$,
∵BC2+MC2=BM2,
∴BC=$\sqrt{B{M}^{2}-M{C}^{2}}$=3$\sqrt{3}$
∴S△ABM=$\frac{1}{2}$AB•BC=$\frac{1}{2}$×12×3$\sqrt{3}$=18$\sqrt{3}$;
(2)解:过O作OE⊥MC,垂足为E,
∵MD是⊙O的弦,OE⊥MD,
∴ME=ED,
又∵∠CEO=∠ECB=∠OBC=90°,
∴四边形OBCE为矩形,
∴CE=OB=6,
又∵MC=x,
∴ME=ED=MC-CE=x-6,MD=2(x-6),
∴CD=MC-MD=x-2(x-6)=12-x,
∴MD•DC=2(x-6)•(12-x)=-2x2+36x-144=-2(x-9)2+18
∵6<x<12,
∴当x=9时,MD•DC的值最大,最大值是18,
∴不存在点M,使MD•DC=20.
点评 此题主要考查了圆的综合应用以及勾股定理以及切线的性质和相似三角形的判定与性质等知识,表示出MD,CD的长是解题关键.

| A. | -1 | B. | 1 | C. | 0 | D. | 2 |
| A. | 9 | B. | -9 | C. | 9或者-9 | D. | 18或者-18 |
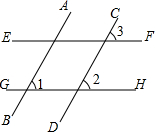 如图,补全下面的说理过程:因为∠2=∠3,所以EF∥GH.理由是:同位角相等,两直线平行.
如图,补全下面的说理过程:因为∠2=∠3,所以EF∥GH.理由是:同位角相等,两直线平行.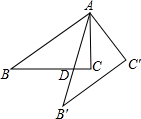 如图,Rt△ABC中,∠ACB=90°,AC=3,BC=4,将△ABC绕点A逆时针旋转得到△AB′C′,AB′与BC相交于点D,当B′C′∥AB时,CD=$\frac{7}{8}$.
如图,Rt△ABC中,∠ACB=90°,AC=3,BC=4,将△ABC绕点A逆时针旋转得到△AB′C′,AB′与BC相交于点D,当B′C′∥AB时,CD=$\frac{7}{8}$.