题目内容
15.(1)解方程:x2-6x+8=0(2)若△ABC三边的长度都满足方程x2-6x+8=0,求此三角形的周长.
分析 (1)因式分解法求解可得x的值;
(2)根据题意分类讨论,结合三角形三边间的关系判断,并求出周长.
解答 解:(1)∵(x-2)(x-4)=0,
∴x-2=0或x-4=0,
解得x1=2,x2=4;
(2)若三边长度分别为2、2、4,则无法构成三角形;
若三边长度分别为2、4、4,则三角形的周长为10;
若三边长度分别为2、2、2,则三角形的周长为6;
若三边长度分别为4、4、4,则三角形的周长为12.
点评 本题主要考查解一元二次方程的能力和三角形三边间的关系,熟练掌握解一元二次方程的几种常用方法:直接开平方法、因式分解法、公式法、配方法,结合方程的特点选择合适、简便的方法是解题的关键.

练习册系列答案
相关题目
8. 如图是一个正方体的展开图,把展开图折叠成正方体后,“我”字一面的相对面上的字是( )
如图是一个正方体的展开图,把展开图折叠成正方体后,“我”字一面的相对面上的字是( )
 如图是一个正方体的展开图,把展开图折叠成正方体后,“我”字一面的相对面上的字是( )
如图是一个正方体的展开图,把展开图折叠成正方体后,“我”字一面的相对面上的字是( )| A. | 梦 | B. | 的 | C. | 国 | D. | 中 |

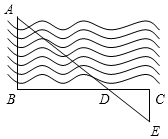 为了估计河的宽度,我们可以在河对岸的岸边选定一个目标记为点A,再在河的这一边选点B和点C,使得AB⊥BC,设BC与AE交于点D,如图所示测得BD=120m,DC=40m,EC=30m,那么这条河的大致宽度是( )
为了估计河的宽度,我们可以在河对岸的岸边选定一个目标记为点A,再在河的这一边选点B和点C,使得AB⊥BC,设BC与AE交于点D,如图所示测得BD=120m,DC=40m,EC=30m,那么这条河的大致宽度是( ) 如图,等腰△EDF的三个的顶点都在等腰△ABC的边上,且∠A=∠B=50°,∠DEF=∠DFE=65°.求证:△EAD≌△DBF.
如图,等腰△EDF的三个的顶点都在等腰△ABC的边上,且∠A=∠B=50°,∠DEF=∠DFE=65°.求证:△EAD≌△DBF.