题目内容

3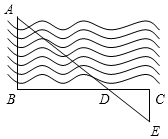．为了估计河的宽度，我们可以在河对岸的岸边选定一个目标记为点A，再在河的这一边选点B和点C，使得AB⊥BC，设BC与AE交于点D，如图所示测得BD=120m，DC=40m，EC=30m，那么这条河的大致宽度是（　　）
A．90mB．60mC．100mD．120m

分析 先证明△ABD∽△ECD，然后利用相似比计算出AB的长即可．

解答 解：∵AB⊥BC，CD⊥BC，
∴△ABD∽△ECD，
∴AB：CE=BD：CD，
即AB：30=120：40，
∴AB=90，
即这条河的大致宽度是90m．
故选A．

点评 本题考查了相似三角形的性质：利用影长测量物体的高度，通常利用相似三角形的性质即相似三角形的对应边的比相等和“在同一时刻物高与影长的比相等”的原理解决．

练习册系列答案
相关题目
16．已知：∠ACB=90°，AC=BC，AD⊥CM，BE⊥CM，垂足分别为D，E，
（1）如图1，
①线段CD和BE的数量关系是CD=BE；
②请写出线段AD，BE，DE之间的数量关系并证明．
（2）如图2，上述结论②还成立吗？如果不成立，请直接写出线段AD，BE，DE之间的数量关系．
17．七年级（1）班的学生分成三个小组，利用星期日的时间去参加公益活动，第一组有学生m名，第二组的学生数比第一组学生数的2倍少10人，第三组的学生数是第二组学生数的一半．
（1）七年级（1）班共有多少名学生？（用含m的式子表示）
（2）若七年级（1）班共有45名学生，求m的值．
14．抛物线y=5（x+2）2-3图象的顶点坐标是（　　）
A．（-3，-2）B．（2，3）C．（-2，3）D．（-2，-3）
1．方程|2x-3y+1|+（3x-y+m）2=0的解满足x＜y，求m的取值范围？
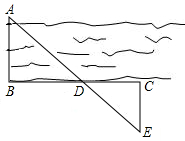8．如图，为了估算河的宽度，我们可以在河对岸选定一个目标作为点A，再在河的这一边选点B和C，使AB⊥BC，然后再选点E，使EC⊥BC，用视线确定BC和AE的交点D，此时如果测得BD=150米，DC=60米，EC=50米，试求两岸间的距离AB．
15．（1）解方程：x2-6x+8=0
（2）若△ABC三边的长度都满足方程x2-6x+8=0，求此三角形的周长．
12．算式（-20）-（+3）-（+5）-（-7）写成省略加号的和的形式正确的为（　　）
A．20+3+5-7B．-20-3-5-7C．-20-3+5+7D．-20-3-5+7
13．如图所示的圆柱，从左边看是（　　）
A．B．C．D．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网