题目内容
18.若直线l1:y=ax+b(a≠0)与直线l2:y=mx+n (m≠0)的交点坐标为(-2,1),则直线l3:y=a(x-3)+b+2(a≠0)与直线l4:y=m(x-3)+n+2(m≠0)的交点坐标为(1,3).分析 把(-2,1)分别代入y=ax+b(a≠0)与y=mx+n (m≠0),得到关于-2a+b=1,-2m+n=1,进而得出2(a-m)=b-n,然后解y=a(x-3)+b+2(a≠0)与y=m(x-3)+n+2(m≠0)所组成的方程组求得x、y的值即可.
解答 解:把(-2,1)分别代入y=ax+b、y=mx+n得-2a+b=1,-2m+n=1,
∴2(a-m)=b-n,
解$\left\{\begin{array}{l}{y=a(x-3)+b+2①}\\{y=m(x-3)+n+2②}\end{array}\right.$
①-②得(a-m)(x-3)+(b-n)=0,
∴x-3=-2,
∴x=1,
把x=1代入y=a(x-3)+b+2得y=-2a+b+2=1+2=3,
∴直线l3:y=a(x-3)+b+2(a≠0)与直线l4:y=m(x-3)+n+2(m≠0)的交点坐标为(1,3),
故答案为(1,3).
点评 本题考查了两条直线相交或平行问题:若直线y=k1x+b1与直线y=k2x+b2平行,则k1=k2;若直线y=k1x+b1与直线y=k2x+b2相交,则由两解析式所组成的方程组的解为交点坐标.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
8.一家商店把一种旅游鞋按成本价a元提高50%标价,然后再以8折优惠卖出,则这种旅游鞋每双的售价是( )
| A. | 0.4a元 | B. | 0.8a元 | C. | 1.2a元 | D. | 1.5a元 |
6.下列关于0的说法中,错误的是( )
| A. | 0是最小的有理数 | B. | 0既不是正数,也不是负数 | ||
| C. | 0的相反数是0 | D. | 0的绝对值是0 |
13.下列事件中,属于随机事件的是( )
| A. | 袋中只有5个黄球,摸出一个球是白球 | |
| B. | 从分别写有2,4,6的三张卡片中随机抽出一张,卡片上的数字能被2整除 | |
| C. | 用长度分别是2cm,3cm,6cm的细木条首尾相连组成一个三角形 | |
| D. | 任意买一张电影票,座位号是偶数 |
10.若一元二次方程x2+2x+a=0有实数根,则a的取值范围是( )
| A. | a≤1 | B. | a≤4 | C. | a<1 | D. | a≥1 |
7.下列式子中,正确的是( )
| A. | |-5|=-5 | B. | -|-5|=5 | C. | -(-5)=-5 | D. | -(-5)=5 |
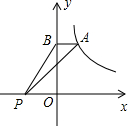 如图,A是反比例函数图象上的一点,过点A作AB⊥y轴于点B,点P在x轴上,△ABP的面积为4,则这个反比例函数的关系式为y=$\frac{8}{x}$.
如图,A是反比例函数图象上的一点,过点A作AB⊥y轴于点B,点P在x轴上,△ABP的面积为4,则这个反比例函数的关系式为y=$\frac{8}{x}$.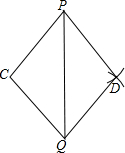 如图,已知△PCQ,按如下步骤作图:①以P为圆心,PC长为半径画弧;②以Q为圆心,QC长为半径画弧,两弧相交于点D;③连接PD、QD.求证:△PCQ≌△PDQ.
如图,已知△PCQ,按如下步骤作图:①以P为圆心,PC长为半径画弧;②以Q为圆心,QC长为半径画弧,两弧相交于点D;③连接PD、QD.求证:△PCQ≌△PDQ.