题目内容
17.计算:(1)($\frac{3x+4}{{{x^2}-1}}$-$\frac{2}{x-1}}$)÷$\frac{x+2}{{{x^2}-2x+1}}$
(2)$\sqrt{3}$×(-$\sqrt{6}}$)+|-$\sqrt{8}}$|+6$\sqrt{\frac{1}{2}}$.
分析 (1)先把括号内通分,再把除法运算化为乘法运算,然后把分子分母分解因式后约分即可;
(2)先进行二次根式的乘法运算,然后化简后合并即可.
解答 解:(1)原式=$[{\frac{3x+4}{{({x+1})({x-1})}}-\frac{2}{x-1}}]×\frac{{{{({x-1})}^2}}}{x+2}$
=$[{\frac{3x+4}{{({x+1})({x-1})}}-\frac{{2({x+1})}}{{({x-1})({x+1})}}}]×\frac{{{{({x-1})}^2}}}{x+2}$
=$\frac{3x+4-2x-2}{{({x+1})({x-1})}}×\frac{{{{({x-1})}^2}}}{x+2}$
=$\frac{x+2}{{({x+1})({x-1})}}×\frac{{{{({x-1})}^2}}}{x+2}$
=$\frac{x-1}{x+1}$;
(2)原式=$-3\sqrt{2}+2\sqrt{2}+3\sqrt{2}$
=$2\sqrt{2}$.
点评 本题考查了二次根式的混合运算:先把二次根式化为最简二次根式,然后进行二次根式的乘除运算,再合并即可.在二次根式的混合运算中,如能结合题目特点,灵活运用二次根式的性质,选择恰当的解题途径,往往能事半功倍.也考查了分式的混合运算.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案
相关题目
18.将0.0000026用科学记数法表示为( )
| A. | 2.6×106 | B. | 0.26×10-5 | C. | 2.6×10-6 | D. | 2.6×10-7 |
19.下列事件中,属于不可能事件的是( )
| A. | 射击运动员射击一次,命中9环 | |
| B. | 今天是星期六,明天就是星期一 | |
| C. | 某种彩票中奖率为10%,买十张有一张中奖 | |
| D. | 在只装有10个红球的布袋中摸出一球,这个球一定是红球 |
7.在一个不透明的盒子里装有40个黑、白两种颜色的球,这些球除颜色外完全相同.小丽做摸球实验,搅匀后她从盒子里摸出一个球记下颜色后,再把球放回盒子中,不断重复上述过程,表是实验中的一组统计数据:
若从盒子里随机摸出一个球,则摸到白球的概率的估计值为0.6.(精确到0.1)
| 摸球的次数n | 100 | 200 | 300 | 500 | 800 | 1000 | 3000 |
| 摸到白球的次数m | 65 | 124 | 178 | 302 | 481 | 599 | 1803 |
| 摸到白球的频率$\frac{m}{n}$ | 0.65 | 0.62 | 0.593 | 0.604 | 0.601 | 0.599 | 0.601 |
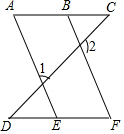 如图,1°∠1+∠2=180°,2°∠A=∠F,3°∠C=∠D,任选两个结论作为条件,说明第三个结论正确,也就是说:
如图,1°∠1+∠2=180°,2°∠A=∠F,3°∠C=∠D,任选两个结论作为条件,说明第三个结论正确,也就是说: 如图,已知∠1=60°,∠2=120°,∠BAC=50°,求∠C的度数.
如图,已知∠1=60°,∠2=120°,∠BAC=50°,求∠C的度数.