题目内容
 如图,直线AB与坐标轴交于A(1,0)、B(0,2)两点,过A,B两点的抛物线与x轴的另一交点为(3,0),P为抛物线上的一动点,当∠PBA=45°时,P点的坐标为
如图,直线AB与坐标轴交于A(1,0)、B(0,2)两点,过A,B两点的抛物线与x轴的另一交点为(3,0),P为抛物线上的一动点,当∠PBA=45°时,P点的坐标为考点:二次函数综合题
专题:
分析:先求出二次函数的解析式,然后过点B作BC⊥BP,交x轴于点C,延长BP交x轴于点D,可得∠CBA=45°,设点C坐标为(a,0),利用面积公式求出a值,然后得出点C坐标,根据BC⊥BD,BO⊥CD,可得△BCO∽DCB,进而得出
=
,求出点D的坐标,然后求出直线BD的解析式,与二次函数解析式联立求出点P的坐标.
| BC |
| CO |
| CD |
| BC |
解答:解:设二次函数的解析式为y=ax2+bx+c,
则
,
解得:
,
二次函数的解析式为:y=
x2-
x+2,
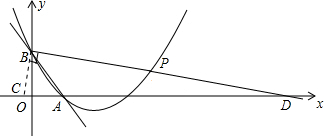 过点B作BC⊥BP,交x轴于点C,延长BP交x轴于点D,
过点B作BC⊥BP,交x轴于点C,延长BP交x轴于点D,
则有∠CBA=45°,
设点C坐标为(a,0)(a<0),
∵S△ABC=
BC•ABsin∠ABC=
AC•BO,
∴
•
•
=
(1-a)•2,
整理得:3a2-16a-12=0,
解得:a=-
或a=6(不合题意,舍去),
∴点C(-
,0),
∵BC⊥BD,BO⊥CD,
∴△BCO∽DCB,
则有
=
,
即BC2=CO•CD,
∴
=
(
+OD),
解得:OD=6,
即点D(6,0),
∵B(0,2),
∴设直线BD的解析式为y=kx+m,
代入得:
,
解得:
,
∴直线BD的解析式为y=-
x+2,
与二次函数的解析式联立得:
,
解得:
,
,
即点P的坐标为(
,
).
故答案为:(
,
).
则
|
解得:
|
二次函数的解析式为:y=
| 2 |
| 3 |
| 8 |
| 3 |
 过点B作BC⊥BP,交x轴于点C,延长BP交x轴于点D,
过点B作BC⊥BP,交x轴于点C,延长BP交x轴于点D,则有∠CBA=45°,
设点C坐标为(a,0)(a<0),
∵S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
∴
| 1 |
| 2 |
| a2+4 |
| 5 |
| ||
| 2 |
| 1 |
| 2 |
整理得:3a2-16a-12=0,
解得:a=-
| 2 |
| 3 |
∴点C(-
| 2 |
| 3 |
∵BC⊥BD,BO⊥CD,
∴△BCO∽DCB,
则有
| BC |
| CO |
| CD |
| BC |
即BC2=CO•CD,
∴
| 40 |
| 9 |
| 2 |
| 3 |
| 2 |
| 3 |
解得:OD=6,
即点D(6,0),
∵B(0,2),
∴设直线BD的解析式为y=kx+m,
代入得:
|
解得:
|
∴直线BD的解析式为y=-
| 1 |
| 3 |
与二次函数的解析式联立得:
|
解得:
|
|
即点P的坐标为(
| 7 |
| 2 |
| 5 |
| 6 |
故答案为:(
| 7 |
| 2 |
| 5 |
| 6 |
点评:本题考查了二次函数的综合知识,涉及到待定系数法求一次函数和二次函数的解析式、三角形的面积公式、相似三角形的判定和性质等知识点,涉及考点众多,综合性较强,计算量大,有一定的难度.

练习册系列答案
 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案
相关题目
 如图所示,用5个小正方体搭成的立体图形,请你从正面、左面、上面观察这个几何体,分别画出你所看到的几何体的形状图.
如图所示,用5个小正方体搭成的立体图形,请你从正面、左面、上面观察这个几何体,分别画出你所看到的几何体的形状图. 如图,在四边形ABCD中,AB∥DC,AH⊥DC于H,CP⊥BD于P,CP延长线分别交AH、AD于E、F,DB平分∠ABC,HE=BP.
如图,在四边形ABCD中,AB∥DC,AH⊥DC于H,CP⊥BD于P,CP延长线分别交AH、AD于E、F,DB平分∠ABC,HE=BP.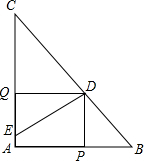 在Rt△ABC中,∠A=90°,AB=6,AC=8,点D为BC的中点,DE⊥BC交边AC与点E,点P为射线AB上一动点,点Q为AC上一动点,且∠PDQ=90°.若BP=2,求CQ的长.
在Rt△ABC中,∠A=90°,AB=6,AC=8,点D为BC的中点,DE⊥BC交边AC与点E,点P为射线AB上一动点,点Q为AC上一动点,且∠PDQ=90°.若BP=2,求CQ的长.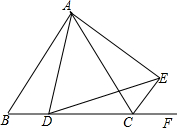 如图,在等边△ABC中,点D为BC边上的一点,在等边△ABC的外角平分线CE上取一点E,使CE=BD,连接AE、DE,请判断△ADE的形状,并说明理由.
如图,在等边△ABC中,点D为BC边上的一点,在等边△ABC的外角平分线CE上取一点E,使CE=BD,连接AE、DE,请判断△ADE的形状,并说明理由.