题目内容
 (1)解方程:2x2-3x=0;
(1)解方程:2x2-3x=0;(2)如图,AC是菱形ABCD的对角线,点E,F分别在AB,AD上,且AE=AF.求证:CE=CF.
考点:菱形的性质,解一元二次方程-因式分解法,全等三角形的判定与性质
专题:
分析:(1)将方程左边的多项式提取公因式x,分解因式后利用两数相乘积为0,两因式中至少有一个为0转化为两个一元一次方程,求出一次方程的解即可得到原方程的解.
(2)根据菱形的性质,利用SAS判定△ACE≌△ACF,从而求得CE=CF.
(2)根据菱形的性质,利用SAS判定△ACE≌△ACF,从而求得CE=CF.
解答:(1)解:x(2x-3)=0,
x=0或2x-3=0,
∴x1=0,x2=
;
(2)证明:∵四边形ABCD是菱形,
∴∠EAC=∠FAC,
又∵AE=AF,AC为公共边,
在△ACE和△ACF中,
,
∴△ACE≌△ACF(SAS),
∴CE=CF.
x=0或2x-3=0,
∴x1=0,x2=
| 3 |
| 2 |
(2)证明:∵四边形ABCD是菱形,
∴∠EAC=∠FAC,
又∵AE=AF,AC为公共边,
在△ACE和△ACF中,
|
∴△ACE≌△ACF(SAS),
∴CE=CF.
点评:(1)此题考查了解一元二次方程-因式分解法,利用因式分解法解方程时,首先将方程右边化为0,左边化为积的形式,然后利用两数相乘积为0,两因式中至少有一个为0转化为两个一元一次方程来求解.
(2)本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、SSA、HL.判定两个三角形全等,先根据已知条件或求证的结论确定三角形,然后再根据三角形全等的判定方法,看缺什么条件,再去证什么条件.
(2)本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、SSA、HL.判定两个三角形全等,先根据已知条件或求证的结论确定三角形,然后再根据三角形全等的判定方法,看缺什么条件,再去证什么条件.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
多项式32x2-x是( )
| A、二次二项式 |
| B、一次一项式 |
| C、四次二项式 |
| D、五次二项式 |
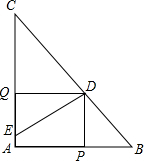 在Rt△ABC中,∠A=90°,AB=6,AC=8,点D为BC的中点,DE⊥BC交边AC与点E,点P为射线AB上一动点,点Q为AC上一动点,且∠PDQ=90°.若BP=2,求CQ的长.
在Rt△ABC中,∠A=90°,AB=6,AC=8,点D为BC的中点,DE⊥BC交边AC与点E,点P为射线AB上一动点,点Q为AC上一动点,且∠PDQ=90°.若BP=2,求CQ的长.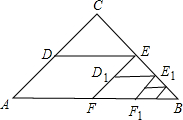 如图,△ABC中,∠C=90°,AC=BC=2,取BC边中点E,作ED∥AB,EF∥AC,得到四边形EDAF,它的面积记作S1;取BE中点E1,作E1D1∥FB,E1F1∥EF,得到四边形E1D1FF1,它的面积记作S2.照此规律作下去,则S2012=
如图,△ABC中,∠C=90°,AC=BC=2,取BC边中点E,作ED∥AB,EF∥AC,得到四边形EDAF,它的面积记作S1;取BE中点E1,作E1D1∥FB,E1F1∥EF,得到四边形E1D1FF1,它的面积记作S2.照此规律作下去,则S2012=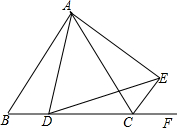 如图,在等边△ABC中,点D为BC边上的一点,在等边△ABC的外角平分线CE上取一点E,使CE=BD,连接AE、DE,请判断△ADE的形状,并说明理由.
如图,在等边△ABC中,点D为BC边上的一点,在等边△ABC的外角平分线CE上取一点E,使CE=BD,连接AE、DE,请判断△ADE的形状,并说明理由.