题目内容
7.若$\frac{(x-1)^{2}}{{x}^{2}-1}=\frac{x-1}{M}$,则M的值是( )| A. | x-1 | B. | x+1 | C. | $\frac{{x}^{2}+1}{2}$ | D. | 1 |
分析 根据分式的分子分母都乘以(或除以)同一个不为零数或(整式),结果不变,可得答案.
解答 解:$\frac{(x-1)^{2}}{{x}^{2}-1}=\frac{x-1}{M}$,得
两边都除以(x-1),
M=x+1,
故选:B.
点评 本题考查了分式的基本性质,分式的分子分母都乘以(或除以)同一个不为零数或(整式),结果不变.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2.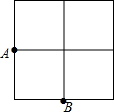 如图,在2×2的正方形网格中有9个格点,已经取定点A和B,在余下的格点中任取一点C,使△ABC为等腰三角形的概率是( )
如图,在2×2的正方形网格中有9个格点,已经取定点A和B,在余下的格点中任取一点C,使△ABC为等腰三角形的概率是( )
 如图,在2×2的正方形网格中有9个格点,已经取定点A和B,在余下的格点中任取一点C,使△ABC为等腰三角形的概率是( )
如图,在2×2的正方形网格中有9个格点,已经取定点A和B,在余下的格点中任取一点C,使△ABC为等腰三角形的概率是( )| A. | $\frac{5}{7}$ | B. | $\frac{2}{5}$ | C. | $\frac{5}{9}$ | D. | $\frac{4}{7}$ |
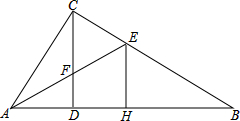 如图,△ABC中,∠ACB=90°,CD⊥AB于点D,E为BC上一点,AE交CD于点F,EH⊥AB于点H,若CF=2FD,EH=$\sqrt{2}$,求CE•BE的值.
如图,△ABC中,∠ACB=90°,CD⊥AB于点D,E为BC上一点,AE交CD于点F,EH⊥AB于点H,若CF=2FD,EH=$\sqrt{2}$,求CE•BE的值. 如图,AC比AB短2cm,BC的垂直平分线交AB于点D,交BC于点E,△ACD的周长是12cm,求AB和AC的长.
如图,AC比AB短2cm,BC的垂直平分线交AB于点D,交BC于点E,△ACD的周长是12cm,求AB和AC的长. 如图所示,已知AB=AC,∠A=40°,AB=10,DC=3,AB的垂直平分线MN交AC于点D,则∠DBC=30度,AD=7.
如图所示,已知AB=AC,∠A=40°,AB=10,DC=3,AB的垂直平分线MN交AC于点D,则∠DBC=30度,AD=7. 如图,AB,AC是⊙O,D是CA延长线上的一点,AD=AB,∠BDC=25°,则∠BOC=100°.
如图,AB,AC是⊙O,D是CA延长线上的一点,AD=AB,∠BDC=25°,则∠BOC=100°.