题目内容
19.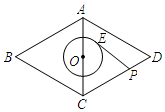 如图,已知菱形ABCD的边长为4,∠B=60°,点O为对角线AC的中点,⊙O
如图,已知菱形ABCD的边长为4,∠B=60°,点O为对角线AC的中点,⊙O半径为1,点P为CD边上一动点,PE与⊙O相切于点E,则PE的最小值是$\sqrt{2}$.
分析 连接BD交AC于O,连接OE、OP.易知PE=$\sqrt{O{P}^{2}-O{E}^{2}}$,因为OE=1,所以OP最小时,PE最小,求出OP的最小值即可解决问题.
解答 解:连接BD交AC于O,连接OE、OP.
∵四边形ABCD是菱形,
∴AC⊥BD,∵∠B=60°,
∴∠ODC=30°,
∵CD=AC=4,
∴OC=2,OD=2$\sqrt{3}$,
∵PE是切线,
∴OE⊥PE,
∴∠OEP=90°,
∴PE=$\sqrt{O{P}^{2}-O{E}^{2}}$,
∵OE=1,
∴OP最小时,PE最小,
当OP⊥CD时,OP=$\frac{OC•OD}{CD}$=$\frac{2×2\sqrt{3}}{4}$=$\sqrt{3}$,
∴PE的最小值=$\sqrt{(\sqrt{3})^{2}-{1}^{2}}$=$\sqrt{2}$.
故答案为$\sqrt{2}$.
点评 本题考查菱形的性质、切线的性质、垂线段最短、勾股定理等知识,解题的关键是灵活运用所学知识解决问题,学会利用垂线段最短解决最值问题,所以中考常考题型.

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案
相关题目
10.下列事件中是必然事件的是( )
| A. | 从一个装满黑球的布袋中摸出一个球是黑球 | |
| B. | 抛掷1枚普通硬币得到正面朝上 | |
| C. | 抛掷1颗正方体骰子得到的点数是偶数 | |
| D. | 抛掷1个普通图钉一定是针尖向下 |
8.若顺次连接四边形的各边中点所得四边形为矩形,则该四边形一定是( )
| A. | 菱形 | B. | 平行四边形 | ||
| C. | 对角线相等的四边形 | D. | 对角线互相垂直的四边形 |
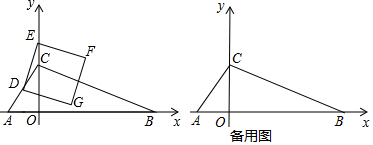
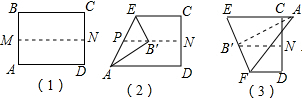
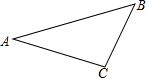 如图,△ABC是直角三角形,∠ACB=90°.
如图,△ABC是直角三角形,∠ACB=90°.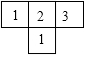 由7个大小相同的小正方体组合成一个几何体.其俯视图如图所示,其中正方形中的数字表示该位置放置的小正方体的个数,则该几何体的左视图为( )
由7个大小相同的小正方体组合成一个几何体.其俯视图如图所示,其中正方形中的数字表示该位置放置的小正方体的个数,则该几何体的左视图为( )