题目内容
14.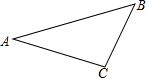 如图,△ABC是直角三角形,∠ACB=90°.
如图,△ABC是直角三角形,∠ACB=90°.(1)尺规作图:作⊙C,使它与AB相切于点D,与AC相交于点E,保留作图痕迹,不写作法,请标明字母.
(2)在(1)中的图中,若BC=4,∠A=30°,求弧DE的长.(结果保留π)
分析 (1)过点C作AB的垂线,垂足为点D,然后以C点为圆心,CD为半径作圆即可;
(2)先根据切线的性质得∠ADC=90°,则利用互余可计算出∠B=∠ACD=60°,再在Rt△BCD中利用∠B的正弦可计算出BC•sinB=$2\sqrt{3}$,然后根据弧长公式求解.
解答 解:(1)所作⊙C,如图所示;
(2)∵⊙C切AB于点D,
∴CD⊥AB,
∴∠ADC=90°,
∵∠ACB=90°,∠A=30°,
∴∠B=∠ACD=60°,
在Rt△BCD中,BC=4,sinB=$\frac{CD}{BC}$,
∴CD=BC•sinB=4×sin60°=$2\sqrt{3}$,
∴弧DE的长为$l=\frac{{60π•2\sqrt{3}}}{180}$=$\frac{{2\sqrt{3}}}{3}π$.
点评 本题考查了作图-复杂作图:复杂作图是在五种基本作图的基础上进行作图,一般是结合了几何图形的性质和基本作图方法;解决此类题目的关键是熟悉基本几何图形的性质,结合几何图形的基本性质把复杂作图拆解成基本作图,逐步操作.也考查了切线的性质和弧长公式.

练习册系列答案
 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案
相关题目
4.下面哪个点在函数y=2x+1的图象上( )
| A. | (2,5) | B. | (-2,1) | C. | (2,0) | D. | (-2,0) |
9.下列几何体中,左视图为三角形的是( )
| A. |  | B. |  | C. |  | D. |  |
6.在数据75,80,80,85,90中,下列结论分析正确的是( )
| A. | 平均数为80 | B. | 中位数为82.5 | C. | 众数为80 | D. | 方差为15 |
3.下列说法中正确的是( )
| A. | 要反映一个家庭每年用于旅游的费用占总支出的百分比宜采用条形统计图 | |
| B. | 打开电视正在播放新闻联播是必然事件 | |
| C. | 方差反映了一组数据的稳定程度 | |
| D. | 检查“天舟一号”飞船各零件的安全性,可采用抽样调查的办法 |




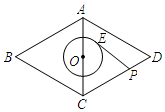 如图,已知菱形ABCD的边长为4,∠B=60°,点O为对角线AC的中点,⊙O
如图,已知菱形ABCD的边长为4,∠B=60°,点O为对角线AC的中点,⊙O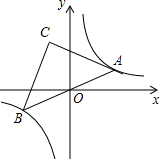 如图,在反比例函数y=$\frac{3}{2x}$的图象上有一动点A,连接AO并延长交图象的另一支于点B,在第二象限内有一点C,满足AC=BC,当点A运动时,点C始终在函数y=$\frac{k}{x}$的图象上运动,若tan∠CAB=2,则k的值为( )
如图,在反比例函数y=$\frac{3}{2x}$的图象上有一动点A,连接AO并延长交图象的另一支于点B,在第二象限内有一点C,满足AC=BC,当点A运动时,点C始终在函数y=$\frac{k}{x}$的图象上运动,若tan∠CAB=2,则k的值为( )