题目内容
12．
如图，已知∠A=∠F，AB∥EF，BC=DE，请说明AD∥CF的理由．
分析 根据平行线的性质得到∠B=∠E，根据全等三角形的性质得到∠ADC=∠FCE，由平行线的判定定理即可得到结论．
解答 证明：∵BC=DE，
∴BD=EC，
∵AB∥EF，
∴∠B=∠E，
在△ABD与△FEC中，$\left\{\begin{array}{l}{∠A=∠F}\\{∠B=∠E}\\{BD=CE}\end{array}\right.$，
∴△ABD≌△FEC，
∴∠ADC=∠FCE，
∴AD∥FC．
点评 此题主要考查了全等三角形的判定与性质，平行线的判定，解决问题的关键是证明△ABD≌△EFC．
练习册系列答案
相关题目
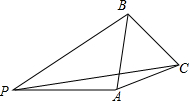如图，P是等边三角形ABC外一点，PA=3，PB=4，PC=5，求∠BPA的度数．
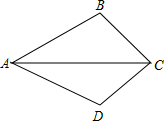已知AB=AD，BC=DC．求证：AC平分∠BAD．
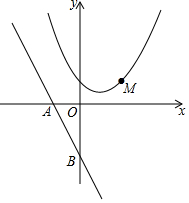直线y=-$\frac{4}{3}$x-4与x轴交于点A，与y轴交于点B，抛物线y=x2-4x+5上的一点M（3，2）．
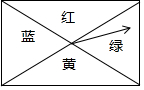如图，一块长宽不等的矩形木板，连接对角线后被分成4个区域，分别涂上红、黄、蓝、绿四色，木板中间装有指针，指针转动停止后，下面两个结论：
1．下列各式中一定是二次根式的是（ ）
| A． | $\root{3}{16}$ | B． | $\sqrt{a}$ | C． | $\sqrt{-{a}^{2}-1}$ | D． | $\sqrt{{a}^{2}+2}$ |