题目内容
12. 如图,AC是正方形ABCD的对角线,将△ACD绕着点A顺时针旋转后得到△AC′D′,点D′落在AC上,C′D′交BC于点E,若AB=1,则图中阴影部分图形的面积是$\sqrt{2}$-1.
如图,AC是正方形ABCD的对角线,将△ACD绕着点A顺时针旋转后得到△AC′D′,点D′落在AC上,C′D′交BC于点E,若AB=1,则图中阴影部分图形的面积是$\sqrt{2}$-1.
分析 根据题意知,将△ACD绕着点A顺时针旋转45°后得到△AC′D′,所以利用等腰直角三角形的面积公式进行解答即可.
解答  解:∵AC是正方形ABCD的对角线,将△ACD绕着点A顺时针旋转后得到△AC′D′,
解:∵AC是正方形ABCD的对角线,将△ACD绕着点A顺时针旋转后得到△AC′D′,
∴∠ACB=∠BC′E=45°,AD′=AD=AB=1,AC=$\sqrt{2}$,∠CD′C′=90°,
∴S阴影=S△ABC-S△ECD′=$\frac{1}{2}$×1×1-$\frac{1}{2}$×($\sqrt{2}$-1)×($\sqrt{2}$-1)=$\sqrt{2}$-1.
故答案是:$\sqrt{2}-1$.
点评 本题考查了旋转的性质,正方形的性质.解题时,需要利用正方形的对角线平分对角和等腰直角三角形的性质.

练习册系列答案
相关题目
5.下列各式正确的是( )
| A. | $\sqrt{81}$=±9 | B. | |3.14-π|=π-3.14 | C. | $\sqrt{-27}$=-9$\sqrt{3}$ | D. | $\sqrt{5}$-$\sqrt{3}$=$\sqrt{2}$ |
4.下列各组中是同类项的是( )
| A. | x与y | B. | 3ab与3abc | C. | 2mn与-2mn | D. | 4x2y与4xy2 |
20.二次函数y=x2+bx+1的对称轴是直线x=-3,则b的值是( )
| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
7.二次函数y=-x2+1的图象与y轴的交点坐标是( )
| A. | (0,1) | B. | (1,0) | C. | (-1,0) | D. | (1,0)或(-1,0) |
4.使二次根式$\sqrt{x-3}$有意义的x的取值范围是( )
| A. | x≠3 | B. | x>3 | C. | x≥3 | D. | x≤3 |
1.方程5x2-2x-$\frac{1}{4}$=x2-2x+$\frac{3}{4}$的根是( )
| A. | x1=-$\frac{1}{2}$,x2=$\frac{1}{2}$ | B. | x1=x2=$\frac{1}{2}$ | C. | x1=-2,x2=2 | D. | x1=-$\frac{1}{4}$,x2=$\frac{1}{4}$ |
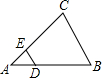 如图,在△ABC中,DE∥BC,DB=2AD,△ADE的面积为1,则四边形DBCE的面积为( )
如图,在△ABC中,DE∥BC,DB=2AD,△ADE的面积为1,则四边形DBCE的面积为( )