题目内容
17．
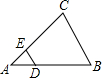如图，在△ABC中，DE∥BC，DB=2AD，△ADE的面积为1，则四边形DBCE的面积为（ ）| A． | 2 | B． | 5 | C． | 6 | D． | 8 |
分析 根据相似三角形的判定与性质，可得△ABC的面积，根据面积的和差，可得答案．
解答 解：由DE∥BC，DB=2AD，得
△ADE∽△ABC，$\frac{AD}{AB}$=$\frac{1}{3}$．
由，△ADE的面积为1，得$\frac{{S}_{△ADE}}{{S}_{△ABC}}$=$\frac{1}{9}$，
得S△ABC=9．
S四边形DBCE=SABC-S△ADE=8，
故选：D．
点评 本题考查了相似三角形的判定与性质，利用相似三角形面积的比等于相似比的平方得出S△ABC=9是解题关键．
练习册系列答案
相关题目
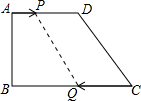直角梯形ABCD中，∠B=90°，AD∥BC，AD=18cm，BC=21cm，点P从点A以1cm/s的速度向点D运动，同时点Q从点C以2cm/s的速度向点B运动．问：
5．下列图形中只是中心对称图形的是（ ）
| A． |  | B． |  | C． |  | D． |  |
如图，AC是正方形ABCD的对角线，将△ACD绕着点A顺时针旋转后得到△AC′D′，点D′落在AC上，C′D′交BC于点E，若AB=1，则图中阴影部分图形的面积是$\sqrt{2}$-1．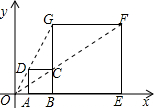
如图，在平面直角坐标系中，正方形ABCD与正方形BEFG是以原点O为位似中心的位似图形，且位似比为$\frac{1}{3}$．点A、B、E在x轴上，若正方形BEFG的边长为6，则C点坐标为（3，2）．
如图，AD∥BE∥CF，直线l1、l2与这三条平行线分别交于点A、B、C和点D、E、F，若AB=3，BC=6，DF=6，则DE的长等于（ ）
如图，直线L1∥L2，圆O与L1和L2分别相切于点A和点B，点M和点N分别是L1和L2上的动点，MN沿L1和L2平移，圆O的半径为1，∠1=60°，当MN与圆相切时，AM的长度等于$\sqrt{3}$或$\frac{\sqrt{3}}{3}$．
________________．