题目内容
12.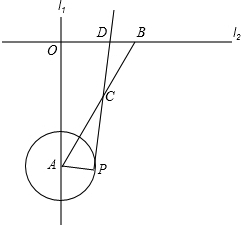 如图,直线l1⊥l2,垂足为O,点A、B分别在直线l1和l2上,∠OAB=30°,OB=2,以A为圆心,1为半径画圆,点P在圆A的圆周上运动,连接AP,过点P画PA的垂线与线段AB相交于点C,与直线l2相交于D,当AC=BC时,OD的长是1或4.
如图,直线l1⊥l2,垂足为O,点A、B分别在直线l1和l2上,∠OAB=30°,OB=2,以A为圆心,1为半径画圆,点P在圆A的圆周上运动,连接AP,过点P画PA的垂线与线段AB相交于点C,与直线l2相交于D,当AC=BC时,OD的长是1或4.
分析 根据l1⊥l2,∠OAB=30°,得到∠OBA=60°,AC=BC=2,由于AP⊥PD,于是得到∠APC=90°,又因为AP=1,得到∠ACP=∠BCD=30°,再根据直角三角形的性质即可得到果.
解答 解:∵l1⊥l2,
∴∠AOB=90°,
∵∠OAB=30°,
∴∠OBA=60°,
∵OB=2,
∴AB=4,
∴AC=BC=2,
∵AP⊥PD,
∴∠APC=90°,
∵AP=1,
∴∠ACP=30°,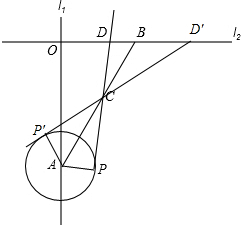
∴∠BCD=30°,
∴∠CDB=90°,
∴BD=$\frac{1}{2}$BC=1,
∴OD=1,
如图,同理∠ACP′=30°,
∴∠BCD′=30°,∵∠ABO=60°,
∴∠BD′C=30°,
∴∠BCD′=∠BD′C,
∴BD′=BC=2,
∴OD′=4,
故答案为:1或4.
点评 本题考查了直角三角形的性质,在直角三角形中,30°的角所对的直角边等于斜边的一半,熟记直角三角形的性质是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
7.如图,在等腰Rt△ABC中,D为斜边AC边上一点,以CD为直角边,点C为直角顶点,向外构造等腰Rt△CDE.动点P从点A出发,以1个单位/s的速度,沿着折线A-D-E运动.在运动过程中,△BCP的面积S与运动时间t(s)的函数图象如图所示,则BC的长是( )
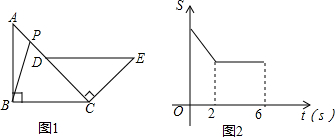

| A. | 2+$\sqrt{2}$ | B. | 4 | C. | 3$\sqrt{2}$ | D. | 2+2$\sqrt{2}$ |
 如图,在梯形ABCD中,AD∥BC,AC与BD交于点O,若S△AOD=4,S△BOC=9,则S梯形ABCD=25.
如图,在梯形ABCD中,AD∥BC,AC与BD交于点O,若S△AOD=4,S△BOC=9,则S梯形ABCD=25.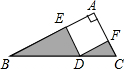 如图,Rt△ABC中,∠A=90°,四边形AEDF为正方形,E、D、F分别在Rt△ABC的三边上,BD=3,CD=2,则图中阴影部分的面积之和为3.
如图,Rt△ABC中,∠A=90°,四边形AEDF为正方形,E、D、F分别在Rt△ABC的三边上,BD=3,CD=2,则图中阴影部分的面积之和为3.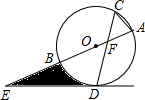 如图,⊙O的直径AB与弦CD相交于点F,且∠ACD=60°,在AB的延长线上取一点E,使得∠AED=30°.
如图,⊙O的直径AB与弦CD相交于点F,且∠ACD=60°,在AB的延长线上取一点E,使得∠AED=30°.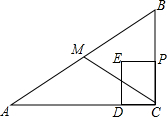 如图,在Rt△ABC中,∠ACB=90°,AC=8cm,BC=6cm,点M是边AB的中点,连结CM,点P从点C出发,以1cm/s的速度沿CB运动到点B停止,以PC为边作正方形PCDE,点D落在线段AC上.设点P的运动时间为t(s).
如图,在Rt△ABC中,∠ACB=90°,AC=8cm,BC=6cm,点M是边AB的中点,连结CM,点P从点C出发,以1cm/s的速度沿CB运动到点B停止,以PC为边作正方形PCDE,点D落在线段AC上.设点P的运动时间为t(s).