Question

13．【探索研究】我们可以借鉴以前研究函数的经验，探索函数y=x+$\frac{1}{x}$（x＞0）的图象性质．
（1）根据下表数据，画出上述函数图象．

X	…	$\frac{1}{4}$	$\frac{1}{3}$	$\frac{1}{2}$	1	2	3	4	…
y	…	$\frac{17}{4}$	$\frac{10}{3}$	$\frac{5}{2}$	2	$\frac{5}{2}$	$\frac{10}{3}$	$\frac{17}{4}$	…

（2）观察图象，写出该函数的一个性质．
【阅读理解】当x＞0时，y=x+$\frac{1}{x}$=${（{\sqrt{x}}）^2}+{（{\sqrt{\frac{1}{x}}}）^2}={（{\sqrt{x}-\sqrt{\frac{1}{x}}}）^2}+2$
（3）由此可见，当x=1时，函数y=x+$\frac{1}{x}$（x＞0）的最小值为2．
【变形应用】
（4）求函数y=x+$\frac{1}{x+1}$（x＞-1）的最小值，并指出y取得最小值时相应的x的值．

Answer 1

分析 （1）根据表格给定数据描点，画出函数图象；
（2）根据函数图象，找出函数的性质；
（3）结合函数图象与【阅读理解】可得出，当x=1时，函数取最小值2，由此即可得出结论；
（4）将函数转化成y=（x+1）+$\frac{1}{x+1}$-1，根据（3）的结论即可得出：当x=0时，函数取最小值1．

解答 解：（1）根据下表数据，画出上述函数图象，如图所示．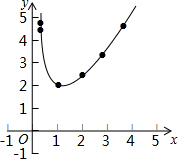
（2）观察函数图象，可得出函数的性质：
当0＜x＜1时，y随x的增大而减小；
当x＞1时，y随x的增大而增大；
当x=1时，y取最小值为2．（写出一个即可）．
（3）结合函数图象与【阅读理解】可得出，当x=1时，函数y=x+$\frac{1}{x}$（x＞0）的最小值为2．
故答案为：1；2．
（4）函数y=x+$\frac{1}{x+1}$=（x+1）+$\frac{1}{x+1}$-1，
∵当x=1时，函数y=x+$\frac{1}{x}$（x＞0）的最小值为2，
∴当x+1=1时，函数y=（x+1）+$\frac{1}{x+1}$-1（x＞-1）的最小值为2-1=1，
此时x=0．
故当x=0时，函数y=x+$\frac{1}{x+1}$（x＞-1）取最小值为1．

点评 本题考查了一次函数综合题，解题的关键是：（1）根据给定数据画出图形；（2）结合函数图象的增减性写出函数的性质；（3）根据给定不等式以及函数图象解决最值问题；（4）将原函数变形为y=（x+1）+$\frac{1}{x+1}$-1．本题属于中档题，难度不大，解决该题型题目时，通过函数图象找出函数的性质是关键．