Question

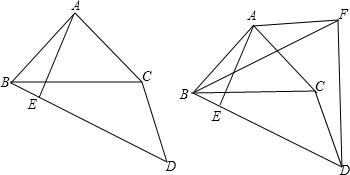
5．如图所示，AB=AC，BD=CD，DE⊥AB交AB的延长线于点E，DF⊥AC交AC的延长线于点F，求证：DE=DF．

Answer 1

分析 根据已知条件证△ABD≌△ACD得AD平分∠EAF，由角平分线性质得DE=DF．

解答 证明：在△ABD和△ACD中，
$\left\{\begin{array}{l}{AB=AC}\\{AD=AD}\\{BD=CD}\end{array}\right.$，
∴△ABD≌△ACD（SSS），
∴∠DAB=∠DAC，即AD平分∠EAF，
又∵DE⊥AE，DF⊥AF，
∴DE=DF．

点评 本题主要考查全等三角形的判定和性质、角平分线的性质，熟悉全等三角形的判定是解题基础，由全等性质得到角相等是关键．