题目内容
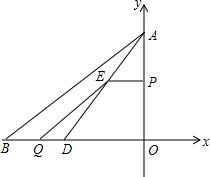 已知:如图,把Rt△ABC放在直角坐标系中,A(0,4)B(-5,0),点D在BC上,且CD=3,现有两个动点P,Q分别从点A和点B同时出发,其中点P以1个单位/秒的速度沿y轴负方向移动,点Q以
已知:如图,把Rt△ABC放在直角坐标系中,A(0,4)B(-5,0),点D在BC上,且CD=3,现有两个动点P,Q分别从点A和点B同时出发,其中点P以1个单位/秒的速度沿y轴负方向移动,点Q以| 5 |
| 4 |
(1)直接写出的PC长度;
(2)当点Q在线段BD上运动时,当x为何值时,△EDQ的面积是△ACD面积的
| 3 |
| 16 |
(3)问:在x轴上是否存在一个点Q,使得△EDQ是直角三角形?若存在,试求点Q的坐标;若不存在,请说明理由.
考点:相似形综合题
专题:
分析:(1)根据点P以1个单位/秒的速度沿y轴负方向移动,AO=4,即可直接得出PC;
(2)过点E作EM⊥CD于点M,先求出BQ=
x,BD=2,得出DQ=2-
x,再根据PE∥x轴,得出EM的值,再根据三角形的面积公式求出S△EDQ和S△ACD的值,最后根据△EDQ的面积是△ACD面积的
,得出
x2-
x+4=
×6,求解即可;
(3)分两种情况讨论:①当∠EQD=90°时,根据EQ∥AC,得出
=
,再代入求出x的值;②当∠QED=90°时,得出△EDQ∽△CDA,
=
,再根据△AEP∽△ADC,得出AE=
x,最后代入求出x的值.
(2)过点E作EM⊥CD于点M,先求出BQ=
| 5 |
| 4 |
| 5 |
| 4 |
| 3 |
| 16 |
| 5 |
| 8 |
| 7 |
| 2 |
| 3 |
| 16 |
(3)分两种情况讨论:①当∠EQD=90°时,根据EQ∥AC,得出
| EQ |
| AC |
| DQ |
| DC |
| ED |
| CD |
| DQ |
| DA |
| 5 |
| 4 |
解答: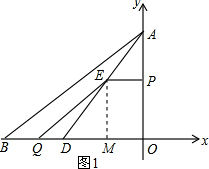 解:(1)∵点P以1个单位/秒的速度沿y轴负方向移动,
解:(1)∵点P以1个单位/秒的速度沿y轴负方向移动,
∴AP=x,
∵A点的坐标是(0,4),
∴AO=4,
∴PC=4-x;
(2)如图1,过点E作EM⊥CD于点M,
∵点Q以
个单位/秒的速度沿x轴正方向移动,
∴BQ=
x,
∵B点的坐标是(-5,0),CD=3,
∴BD=2,
∴DQ=2-
x,
∵PE∥x轴,
∴EM=PC=4-x,
∴S△EDQ=
QD•EM=
(2-
x)(4-x)=
x2-
x+4,
∵S△ACD=
CD•AC=
×4×3=6,
若△EDQ的面积是△ACD面积的
,
则
x2-
x+4=
×6,
解得:x1=1,x2=
(舍去),
当点Q在线段BD上运动时,当x为1时,△EDQ的面积是△ACD面积的
;
(3)分两种情况讨论:
①如图2,当∠EQD=90°时,显然有EQ=PC=4-x,
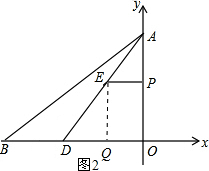 ∵EQ∥AC,
∵EQ∥AC,
∴△EDQ∽△ADC
∴
=
,
即
=
,
解得x=2.5
②如图3,当∠QED=90°时,
∵∠CDA=∠EDQ,∠QED=∠C=90°,
∴△EDQ∽△CDA,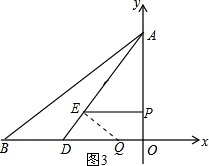
∴
=
,
∵△AEP∽△ADC,
∴
=
,
∴
=
,
∴AE=
x,
∴ED=5-
x,
∴
=
,
解得x=3.1,
综上所述,当x为2.5秒或3.1秒时,△EDQ为直角三角形.
 解:(1)∵点P以1个单位/秒的速度沿y轴负方向移动,
解:(1)∵点P以1个单位/秒的速度沿y轴负方向移动,∴AP=x,
∵A点的坐标是(0,4),
∴AO=4,
∴PC=4-x;
(2)如图1,过点E作EM⊥CD于点M,
∵点Q以
| 5 |
| 4 |
∴BQ=
| 5 |
| 4 |
∵B点的坐标是(-5,0),CD=3,
∴BD=2,
∴DQ=2-
| 5 |
| 4 |
∵PE∥x轴,
∴EM=PC=4-x,
∴S△EDQ=
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 4 |
| 5 |
| 8 |
| 7 |
| 2 |
∵S△ACD=
| 1 |
| 2 |
| 1 |
| 2 |
若△EDQ的面积是△ACD面积的
| 3 |
| 16 |
则
| 5 |
| 8 |
| 7 |
| 2 |
| 3 |
| 16 |
解得:x1=1,x2=
| 23 |
| 5 |
当点Q在线段BD上运动时,当x为1时,△EDQ的面积是△ACD面积的
| 3 |
| 16 |
(3)分两种情况讨论:
①如图2,当∠EQD=90°时,显然有EQ=PC=4-x,
 ∵EQ∥AC,
∵EQ∥AC,∴△EDQ∽△ADC
∴
| EQ |
| AC |
| DQ |
| DC |
即
| 4-x |
| 4 |
| ||
| 3 |
解得x=2.5
②如图3,当∠QED=90°时,
∵∠CDA=∠EDQ,∠QED=∠C=90°,
∴△EDQ∽△CDA,

∴
| ED |
| CD |
| DQ |
| DA |
∵△AEP∽△ADC,
∴
| AE |
| AD |
| AP |
| AC |
∴
| AE |
| 5 |
| x |
| 4 |
∴AE=
| 5 |
| 4 |
∴ED=5-
| 5 |
| 4 |
∴
5-
| ||
| 3 |
| ||
| 5 |
解得x=3.1,
综上所述,当x为2.5秒或3.1秒时,△EDQ为直角三角形.
点评:此题考查了相似形的综合,用到的知识点是相似三角形的判定与性质、勾股定理,关键是根据题意画出图形,注意分两种情况讨论.

练习册系列答案
相关题目
在下列关系式中,y是x的二次函数的关系式是( )
| A、8xy+x2=1 |
| B、y2-ax+2=0 |
| C、y+5x2-2=0 |
| D、2x2-y2+4=0 |
下列运算正确的是( )
A、(
| ||||||
B、(
| ||||||
C、(
| ||||||
D、2a-2=
|
如果等腰三角形的两边长是6cm和3cm,那么它的周长是( )
| A、9cm |
| B、12cm |
| C、12cm或15cm |
| D、15cm |
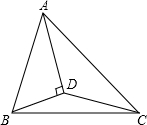 如图,已知S△ABC=8m2,AD平分∠BAC,且AD⊥BD于点D,则S△ADC=
如图,已知S△ABC=8m2,AD平分∠BAC,且AD⊥BD于点D,则S△ADC= 如图,已知直线AB经过x轴上的点A(2,0)且与抛物线y=ax2相交于B、C两点,已知点B坐标为(1,1)
如图,已知直线AB经过x轴上的点A(2,0)且与抛物线y=ax2相交于B、C两点,已知点B坐标为(1,1)