题目内容
分解因式:
(1)x2y-4xy+4y.
(2)9(a+b)2-(a-b)2.
(3)12a2b-18ab2-24a3b3.
(4)4a(x-2)2-2b(2-x)3.
(5)a(a-2b)(2a-3b)-2b(2b-a)(3b-2a)
(1)x2y-4xy+4y.
(2)9(a+b)2-(a-b)2.
(3)12a2b-18ab2-24a3b3.
(4)4a(x-2)2-2b(2-x)3.
(5)a(a-2b)(2a-3b)-2b(2b-a)(3b-2a)
考点:提公因式法与公式法的综合运用
专题:
分析:(1)首先提取公因式y,进而利用完全平方公式分解因式即可;
(2)直接利用平方差公式分解因式即可;
(3)首先提取公因式6ab,进而分解因式即可;
(4)首先提取公因式2(2-x)2,进而分解因式得出即可;
(5)直接利用提取公因式分解因式得出即可.
(2)直接利用平方差公式分解因式即可;
(3)首先提取公因式6ab,进而分解因式即可;
(4)首先提取公因式2(2-x)2,进而分解因式得出即可;
(5)直接利用提取公因式分解因式得出即可.
解答:解:(1)x2y-4xy+4y=y(x2-4x+4)=y(x-2)2;
(2)9(a+b)2-(a-b)2,
=[3(a+b)]2-(a-b)2,
=[3(a+b)+(a-b)][3(a+b)-(a-b)],
=(4a+2b)(2a+4b),
=4(2a+b)(a+2b);
(3)原式=6ab(2a-3b-4a2b2);
(4)4a(x-2)2-2b(2-x)3
=4a(2-x)2-2b(2-x)3
=2(2-x)2[2a-b(2-x)]
=2(2-x)2(2a-2b+bx);
(5)原式=a(a-2b)(2a-3b)-2b(a-2b)(2a-3b),
=(a-2b)(2a-3b)(a-2b),
=(a-2b)2(2a-3b).
(2)9(a+b)2-(a-b)2,
=[3(a+b)]2-(a-b)2,
=[3(a+b)+(a-b)][3(a+b)-(a-b)],
=(4a+2b)(2a+4b),
=4(2a+b)(a+2b);
(3)原式=6ab(2a-3b-4a2b2);
(4)4a(x-2)2-2b(2-x)3
=4a(2-x)2-2b(2-x)3
=2(2-x)2[2a-b(2-x)]
=2(2-x)2(2a-2b+bx);
(5)原式=a(a-2b)(2a-3b)-2b(a-2b)(2a-3b),
=(a-2b)(2a-3b)(a-2b),
=(a-2b)2(2a-3b).
点评:此题主要考查了提取公因式法以及公式法分解因式,熟练应用乘法公式是解题关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
在-|-2|,|-(-3)|,+(-2),-(-6),-[-(-2)],+[-(+5)]中,负数有( )(先化简)
| A、1个 | B、2个 | C、3个 | D、4个 |
 如图,AB是⊙O的直径,DC是弦,若∠BDC=31°,则∠COB的度数等于( )
如图,AB是⊙O的直径,DC是弦,若∠BDC=31°,则∠COB的度数等于( )| A、64° | B、60° |
| C、62° | D、65° |
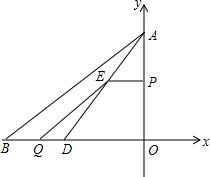 已知:如图,把Rt△ABC放在直角坐标系中,A(0,4)B(-5,0),点D在BC上,且CD=3,现有两个动点P,Q分别从点A和点B同时出发,其中点P以1个单位/秒的速度沿y轴负方向移动,点Q以
已知:如图,把Rt△ABC放在直角坐标系中,A(0,4)B(-5,0),点D在BC上,且CD=3,现有两个动点P,Q分别从点A和点B同时出发,其中点P以1个单位/秒的速度沿y轴负方向移动,点Q以