题目内容
 如图,△ABC绕顶点A逆时针旋转30°至△ADE,∠B=40°,∠DAC=50°,则∠E=
如图,△ABC绕顶点A逆时针旋转30°至△ADE,∠B=40°,∠DAC=50°,则∠E=考点:旋转的性质
专题:计算题
分析:先根据旋转的性质得∠D=∠B=40°,∠CAE=30°,则∠DAE=∠DAC+∠CAE=80°,然后在△ADE中利用三角形内角和定理计算∠E的度数.
解答:解:∵△ABC绕顶点A逆时针旋转30°至△ADE,
∴∠D=∠B=40°,∠CAE=30°,
而∠DAC=50°,
∴∠DAE=∠DAC+∠CAE=80°,
在△ADE中,∠E=180°-∠DAE-∠ADE=180°-80°-40°=60°.
故答案为60°.
∴∠D=∠B=40°,∠CAE=30°,
而∠DAC=50°,
∴∠DAE=∠DAC+∠CAE=80°,
在△ADE中,∠E=180°-∠DAE-∠ADE=180°-80°-40°=60°.
故答案为60°.
点评:本题考查了旋转的性质:旋转前后两图形全等;对应点到旋转中心的距离相等;对应点与旋转中心的连线段的夹角等于旋转角.也考查了三角形内角和定理.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
实数m,n满足mn=1,记P=
+
,Q=
+
,则P、Q的大小关系为( )
| 1 |
| 1+m |
| 1 |
| 1+n |
| m |
| 1+m |
| n |
| 1+n |
| A、P>Q | B、P=Q |
| C、P<Q | D、不确定 |
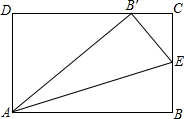 如图,矩形ABCD的长AB=5,宽BC=4,E在BC上,连结AE,把△ABE沿AE对折,使B正好落在DC边B′处.那么AE=
如图,矩形ABCD的长AB=5,宽BC=4,E在BC上,连结AE,把△ABE沿AE对折,使B正好落在DC边B′处.那么AE= 如图,在△ABC中,分别以AC,BC为边作等边△ACD和等边△BCE.设△ACD、△BCE、△ABC的面积分别是S1、S2、S3,现有如下结论:
如图,在△ABC中,分别以AC,BC为边作等边△ACD和等边△BCE.设△ACD、△BCE、△ABC的面积分别是S1、S2、S3,现有如下结论: 如图,将矩形ABCD绕点C沿顺时针方向旋转90°到矩形A′B′CD′的位置,AB=2,AD=4,则阴影部分的面积为
如图,将矩形ABCD绕点C沿顺时针方向旋转90°到矩形A′B′CD′的位置,AB=2,AD=4,则阴影部分的面积为