题目内容
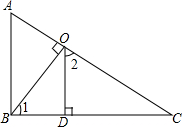 如图,∠ABC=90°,∠1=52°,过点B作AC的垂线BO,垂足为O,过O作BC的垂线,垂足为D,若∠1=∠2,求∠ABO、∠BOD、∠BDO的度数.
如图,∠ABC=90°,∠1=52°,过点B作AC的垂线BO,垂足为O,过O作BC的垂线,垂足为D,若∠1=∠2,求∠ABO、∠BOD、∠BDO的度数.考点:直角三角形的性质
专题:
分析:由∠ABC=90°,∠1=52°,可得∠ABO=90°-∠1,由直角三角形两锐角互余可得∠BOD=90°-∠1,根据垂直定义可得∠BDO=90°.
解答:
解:∵∠ABC=90°,∠1=52°,
∴∠ABO=∠ABC-∠1=90°-52°=38°,
∵OD⊥BC于D,
∴∠BDO=90°,∠BOD=90°-∠1=38°.
∴∠ABO=∠ABC-∠1=90°-52°=38°,
∵OD⊥BC于D,
∴∠BDO=90°,∠BOD=90°-∠1=38°.
点评:本题考查了直角三角形的性质:在直角三角形中,两个锐角互余.也考查了垂直的定义,牢记定义与性质是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图所示,在Rt△ABC中,∠C=90°,AD为∠CAB的平分线,CD=3厘米,则点D到AB的距离为( )
如图所示,在Rt△ABC中,∠C=90°,AD为∠CAB的平分线,CD=3厘米,则点D到AB的距离为( )| A、3厘米 | B、6厘米 |
| C、9厘米 | D、不能确定 |
下列说法中不正确的是( )
| A、全等三角形的周长相等 |
| B、全等三角形的面积相等 |
| C、全等三角形一定能够重合 |
| D、全等三角形一定关于某直线对称 |
方程x2+3x-4=0的根的情况是( )
| A、有两个不相等的实数根 |
| B、没有实数根 |
| C、有两个相等的实数根 |
| D、有一个实数根 |
下列计算正确的是( )
| A、x3+2x2=3x5 |
| B、(-3x3)2=6x6 |
| C、(-x)4÷(-x)2=-x2 |
| D、(-x3)•(-x)2=-x5 |
 如图,A,B,C,D,P是⊙O上的五个点,且∠APB=∠CPD.
如图,A,B,C,D,P是⊙O上的五个点,且∠APB=∠CPD.
 如图,一架25m的云梯AB斜靠在一竖直的墙AO上,这时AO为24m
如图,一架25m的云梯AB斜靠在一竖直的墙AO上,这时AO为24m 已知B,A,D在同一条直线上,∠1=∠C,∠B=40°,求∠BAE的度数.
已知B,A,D在同一条直线上,∠1=∠C,∠B=40°,求∠BAE的度数.