题目内容
如图,在梯形ABCD中,AB∥CD.
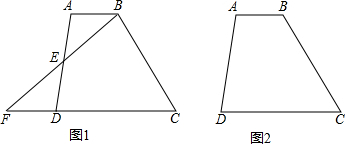
(1)如图1,若点E为AD的中点,BE的延长线交CD的延长线交于点F,求证:S梯形ABCD=S△CBF.
(2)如图2,请过点B画一条直线将梯形ABCD的面积平分,并简单说出画法.

(1)如图1,若点E为AD的中点,BE的延长线交CD的延长线交于点F,求证:S梯形ABCD=S△CBF.
(2)如图2,请过点B画一条直线将梯形ABCD的面积平分,并简单说出画法.
考点:梯形,三角形的面积
专题:
分析:(1)首先根据AAS证明△BAE≌△FDE,所以S△BAE=S△FDE,进而可得S梯形ABCD=S△CBF.
(2)取AD的中点M,连接DE并延长,交CB的延长线于点N,则S梯形ABCD=S△CDF,再取CN的中点G,作直线BG,则S△CBG=S△FBG=S梯形ABGD=
S梯形ABCD,故直线BG即可将这块试验田分割成面积相等的两块.
(2)取AD的中点M,连接DE并延长,交CB的延长线于点N,则S梯形ABCD=S△CDF,再取CN的中点G,作直线BG,则S△CBG=S△FBG=S梯形ABGD=
| 1 |
| 2 |
解答:(1)证明:∵E是AD的中点,
∴AE=DE.
∵AB∥DC,
∴∠ABE=∠DFE.
在△BAE与△FDE中,
,
∴△BAE≌△FDE(AAS),
∴S△BAE=S△FBE,
∴S梯形ABCD=S△CBF.
(2)取AD的中点M,连接DE并延长,交CB的延长线于点N,则S梯形ABCD=S△CDF,再取CN的中点G,作直线BG,如图所示:

∴AE=DE.
∵AB∥DC,
∴∠ABE=∠DFE.
在△BAE与△FDE中,
|
∴△BAE≌△FDE(AAS),
∴S△BAE=S△FBE,
∴S梯形ABCD=S△CBF.
(2)取AD的中点M,连接DE并延长,交CB的延长线于点N,则S梯形ABCD=S△CDF,再取CN的中点G,作直线BG,如图所示:

点评:本题考查了三角形的面积,全等三角形的判定与性质,梯形的性质,作图-应用与设计作图,(2)中通过作辅助线构造全等三角形是解题的关键.

练习册系列答案
 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
判断两个直角三角形全等的方法不正确的有( )
| A、两条直角边对应相等 |
| B、斜边和一锐角对应相等 |
| C、斜边和一条直角边对应相等 |
| D、两个锐角对应相等 |
 如图所示,△ABC的三个顶点分别在直线a、b上,且a∥b,若∠1=110°,∠2=70°,则∠3的度数是( )
如图所示,△ABC的三个顶点分别在直线a、b上,且a∥b,若∠1=110°,∠2=70°,则∠3的度数是( )| A、40° | B、50° |
| C、60° | D、70° |
 如图,等腰三角形ABC,AB=AC、∠BAC=30°,以AB为直径的⊙O交AC于点D,连接BD,求∠CBD.
如图,等腰三角形ABC,AB=AC、∠BAC=30°,以AB为直径的⊙O交AC于点D,连接BD,求∠CBD. 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论中:
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论中: 一次数学活动课上,小聪将一副三角板按图中方式叠放,则∠α等于
一次数学活动课上,小聪将一副三角板按图中方式叠放,则∠α等于