题目内容
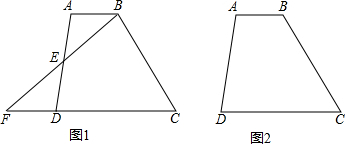
一次数学活动课上，小聪将一副三角板按图中方式叠放，则∠α等于考点：三角形的外角性质
专题：
分析：先根据直角三角板的性质求出∠A，∠ABC，∠C，∠CDE与∠E的度数，再由三角形外角的性质即可得出结论．
解答：
解：∵图中是一副直角三角板，
∴∠A=∠ABC=45°，∠C=90°，∠CDE=60°，∠E=30°．
∵∠ADF是△CDE的外角，
∴∠ADF=∠C+∠E=90°+30°=120°．
∵∠α是△ADF的外角，
∴∠α=∠A+∠ADF=45°+120°=165°．
故答案为：165．
解：∵图中是一副直角三角板，∴∠A=∠ABC=45°，∠C=90°，∠CDE=60°，∠E=30°．
∵∠ADF是△CDE的外角，
∴∠ADF=∠C+∠E=90°+30°=120°．
∵∠α是△ADF的外角，
∴∠α=∠A+∠ADF=45°+120°=165°．
故答案为：165．
点评：本题考查的是三角形外角的性质，熟知三角形的一个外角等于和它不相邻的两个内角的和是解答此题的关键．
练习册系列答案
阅读快车系列答案
相关题目
如图，A、B、C、D是同一直线l上的四点，则AD-AB=抛物线y=-（x+3）2-5的开口方向，对称轴，顶点坐标分别是（ ）
| A、开口向上；x=-3；（-3，5） |
| B、开口向上；x=3；（3，5） |
| C、开口向下；x=3；（-3，-5） |
| D、开口向下；x=-3；（-3，-5） |
如果一个三角形的一内角平分线垂直于对边，那么这个三角形一定是（ ）
| A、等腰三角形 | B、等边三角形 |
| C、锐角三角形 | D、不能确定 |
如果两个相似三角形对应边的比是3：4，那么它们的对应高的比是（ ）
| A、9：16 | ||
B、
| ||
| C、3：4 | ||
| D、3：7 |
已知有理数a大于有理数b，则（ ）
| A、a的绝对值大于b的绝对值 |
| B、a的绝对值小于b的绝对值 |
| C、a的相反数大于b的相反数 |
| D、a的相反数小于b的相反数 |
已知点A（2，a）在反比例函数y=
的图象上，则a的值是（ ）
| -4 |
| x |
| A、2 | ||
| B、-2 | ||
| C、-4 | ||
D、
|