题目内容
8.已知点O是平面直角坐标系的原点,直线y=2x+b(b>0)交x轴于点A,交y轴于点B,点P(m,n)是线段AB上一点,且OP平分∠AOB,双曲线y=$\frac{2}{x}$与直线y=2x+b(b>0)在第一象限的交点为点M,若S△MOP=3S△AOP,求b的值.分析 作PG⊥x轴于G,PN⊥y轴于N,MH⊥y轴于H,根据角平分线的性质定理可知PG=PN,从而求得n=-m,根据直线解析式求得A、B的坐标,得出OA、OB的值,进而得出2S△AOP=S△BOP,由S△MOP=3S△AOP,得出2S△MOP=S△BOP,从而求得MH=$\frac{1}{2}$PN=$\frac{1}{2}$n=-$\frac{1}{2}$m=$\frac{1}{6}$b,代入反比例函数的解析式求得M点的坐标,把M的坐标代入直线的解析式得出关于b的方程,解方程即可求得b的值.
解答 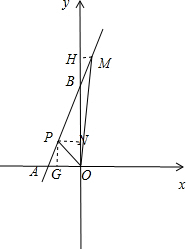 解:如图,作PG⊥x轴于M,PN⊥y轴于N,MH⊥y轴于H,
解:如图,作PG⊥x轴于M,PN⊥y轴于N,MH⊥y轴于H,
∵OP平分∠AOB,
∴PG=PN,
∵P(m,n),
∴n=-m,
∴-m=2m+b,
∴m=-$\frac{1}{3}$b,
∵直线y=2x+b(b>0)交x轴于点A,交y轴于点B,
∴A(-$\frac{b}{2}$,0),B(0,b),
∴OB=2OA,
∴2S△AOP=S△BOP,
∵S△MOP=3S△AOP,
∴2S△MOP=S△BOP
∴MH=$\frac{1}{2}$PN=$\frac{1}{2}$n=-$\frac{1}{2}$m=$\frac{1}{6}$b,
∴M的横坐标为$\frac{1}{6}$b,代入y=$\frac{2}{x}$得y=$\frac{12}{b}$,
∴M($\frac{b}{6}$,$\frac{12}{b}$),
∵M是直线y=2x+b上的点,
∴$\frac{12}{b}$=2×$\frac{b}{6}$+b,
解得b=±3,
∵b>0,
∴b=3.
点评 本题考查了反比例函数和一次函数的交点问题,角平分线的性质定理,三角形面积等,交点坐标适合两个解析式是本题的关键.

练习册系列答案
 作业辅导系列答案
作业辅导系列答案
相关题目
19.实数-27的立方根为( )
| A. | ±3 | B. | 3 | C. | -3 | D. | 没有立方根 |
16.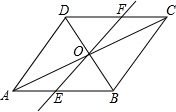 如图,在平行四边形ABCD中,对角线AC,BD并于点O,经过点O的直线交AB于E,交CD于F.
如图,在平行四边形ABCD中,对角线AC,BD并于点O,经过点O的直线交AB于E,交CD于F.
①求证:OE=OF.
②连接DE,BF,则EF与BD满足什么条件时,四边形DEBF是矩形?请说明理由.
 如图,在平行四边形ABCD中,对角线AC,BD并于点O,经过点O的直线交AB于E,交CD于F.
如图,在平行四边形ABCD中,对角线AC,BD并于点O,经过点O的直线交AB于E,交CD于F.①求证:OE=OF.
②连接DE,BF,则EF与BD满足什么条件时,四边形DEBF是矩形?请说明理由.
18.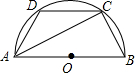 如图,AB是半圆O的直径,D是$\widehat{AC}$上一点,若∠BAC=35°,则∠ADC的度数是( )
如图,AB是半圆O的直径,D是$\widehat{AC}$上一点,若∠BAC=35°,则∠ADC的度数是( )
 如图,AB是半圆O的直径,D是$\widehat{AC}$上一点,若∠BAC=35°,则∠ADC的度数是( )
如图,AB是半圆O的直径,D是$\widehat{AC}$上一点,若∠BAC=35°,则∠ADC的度数是( )| A. | 100° | B. | 120° | C. | 125° | D. | 130° |
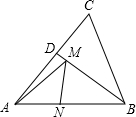 如图,在锐角三角形ABC中,AB=2,∠ABC=60°,∠ABC的平分线交AC于D,M、N分别是BD、AB上的动点,则AM+MN的最小值是$\sqrt{3}$.
如图,在锐角三角形ABC中,AB=2,∠ABC=60°,∠ABC的平分线交AC于D,M、N分别是BD、AB上的动点,则AM+MN的最小值是$\sqrt{3}$.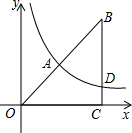 如图,平面直角坐标系中,点B在第一象限,OC=BC,∠OCB=90°,OB=4$\sqrt{2}$,且反比例函数y=$\frac{m}{x}$(m≠0)的图象经过OB的中点A.
如图,平面直角坐标系中,点B在第一象限,OC=BC,∠OCB=90°,OB=4$\sqrt{2}$,且反比例函数y=$\frac{m}{x}$(m≠0)的图象经过OB的中点A.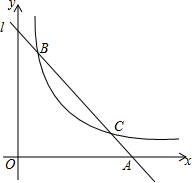 如图,直线l与双曲线y=$\frac{k}{x}$(x>0)交于B,C两点,与x轴交于点A,连接BO,△AOB的面积为6.
如图,直线l与双曲线y=$\frac{k}{x}$(x>0)交于B,C两点,与x轴交于点A,连接BO,△AOB的面积为6.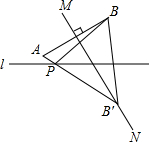 如图,已知点B关于直线l的对称点是B′,AB的垂直平分线MN交BB′于B′,AB′交直线l于点P,点B到直线l的距离为3cm,求PA+PB的值.
如图,已知点B关于直线l的对称点是B′,AB的垂直平分线MN交BB′于B′,AB′交直线l于点P,点B到直线l的距离为3cm,求PA+PB的值.