题目内容
13.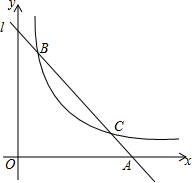 如图,直线l与双曲线y=$\frac{k}{x}$(x>0)交于B,C两点,与x轴交于点A,连接BO,△AOB的面积为6.
如图,直线l与双曲线y=$\frac{k}{x}$(x>0)交于B,C两点,与x轴交于点A,连接BO,△AOB的面积为6.(1)若B、C两点的横坐标分别为1、3,求k的值;
(2)若B、C两点的横坐标分别为a、2a,求k的值.
分析 (1)作BD⊥x轴于D,CE⊥x轴于E,如图,根据反比例函数图象上点的坐标特征得到B(1,k),B(3,$\frac{k}{3}$),则OD=1,DE=2,BD=3CE,根据三角形相似对应边成比例,得到AE=1,然后根据三角形面积公式计算k的值.
(2)根据反比例函数图象上点的坐标特征得到B(a,$\frac{k}{a}$),B(2a,$\frac{k}{2a}$),则OD=a,DE=a,BD=2CE,所以CE为△ABD的中位线,得到AE=DE=a,然后根据三角形面积公式计算k的值.
解答  解:(1)作BD⊥x轴于D,CE⊥x轴于E,如图,
解:(1)作BD⊥x轴于D,CE⊥x轴于E,如图,
∵B、C两点的横坐标分别为1、3,
∴B(1,k),B(3,$\frac{k}{3}$),
∴OD=1,DE=2,BD=3CE,
∵CE∥BD,
∴△ACE∽△ABD,
∴$\frac{AE}{AE+DE}$=$\frac{CE}{BD}$=$\frac{1}{3}$,
∴$\frac{AE}{AE+2}$=$\frac{1}{3}$,
∴AE=1,
∴OA=4,
∵△AOB的面积为6,
∴$\frac{1}{2}$×4•k=6,
∴k=3.
(2)作BD⊥x轴于D,CE⊥x轴于E,如图,
∵B、C两点的横坐标分别为a、2a,
∴B(a,$\frac{k}{a}$),B(2a,$\frac{k}{2a}$),
∴OD=a,DE=a,BD=2CE,
∴CE为△ABD的中位线,
∴AE=DE=a,
∴OA=3a,
∵△AOB的面积为6,
∴$\frac{1}{2}$•3a•k=6,
∴k=$\frac{4}{a}$.
点评 本题考查了反比例函数和一次函数的交点问题以及反比例函数系数k的几何意义:在反比例函数y=$\frac{k}{x}$图象中任取一点,过这一个点向x轴和y轴分别作垂线,与坐标轴围成的矩形的面积是定值|k|.

 阅读快车系列答案
阅读快车系列答案| A. | -4的立方是64 | B. | 0.1的立方根是0.001 | ||
| C. | 4的算术平方根是16 | D. | 9的平方根是±3 |
| A. | a+b<0 | B. | a+b=0 | C. | a+b>0 | D. | 以上都不对 |
| A. | 30° | B. | 45° | C. | 60° | D. | 80° |
| A. | $\frac{1}{2}$ | B. | -2 | C. | 0 | D. | -$\frac{1}{2}$ |