题目内容
9.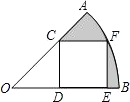 如图,在半径为$\sqrt{10}$,圆心角等于45°的扇形AOB内部作一个正方形CDEF,使点C在OA上,点D、E在OB上,点F在弧AB上,则阴影部分的面积为$\frac{5π}{4}$-3.(结果保留π)
如图,在半径为$\sqrt{10}$,圆心角等于45°的扇形AOB内部作一个正方形CDEF,使点C在OA上,点D、E在OB上,点F在弧AB上,则阴影部分的面积为$\frac{5π}{4}$-3.(结果保留π)
分析 阴影部分的面积即为半径为$\sqrt{10}$,圆心角等于45°的扇形AOB面积减去正方形的面积和等腰直角三角形的面积.
解答  解:连接OF,
解:连接OF,
∵∠AOD=45°,四边形CDEF是正方形,
∴OD=CD=DE=EF,
于是在Rt△OFE中,OE=2EF,
∵OF=$\sqrt{10}$,EF2+OE2=OF2,
∴EF2+(2EF)2=10,
解得:EF=$\sqrt{2}$,
∴EF=OD=CD=$\sqrt{2}$,
∴S阴影=S扇形OAB-S△OCD-S正方形CDEF=$\frac{45π•10}{360}$-$\frac{1}{2}×\sqrt{2}×\sqrt{2}$-$\sqrt{2}×\sqrt{2}$=$\frac{5π}{4}$-3,
故答案为:$\frac{5π}{4}$-3.
点评 本题考查了扇形面积的计算,弧长的计算,熟练掌握弧长公式l=$\frac{nπr}{180}$,是解题的关键.

练习册系列答案
相关题目
20.某厂今年3月的产值为72万元,5月下降到50万元,这两个月平均每月降低的百分率是多少?若设平均每月降低的百分率为x,则列出方程是( )
| A. | 50(1+x)=72 | B. | 50(1+x)+50(1+x)2=72 | C. | 50(1-x)2=72 | D. | 72(1-x)2=50 |
17. 如图,一条公路修到湖边时,需拐弯绕道而过,如果第一次拐的角∠A是100°第二次拐的角∠B是150°,第三次拐的角是∠C,这时的道路恰好和第一次拐弯之前的道路平行,则∠C是( )
如图,一条公路修到湖边时,需拐弯绕道而过,如果第一次拐的角∠A是100°第二次拐的角∠B是150°,第三次拐的角是∠C,这时的道路恰好和第一次拐弯之前的道路平行,则∠C是( )
 如图,一条公路修到湖边时,需拐弯绕道而过,如果第一次拐的角∠A是100°第二次拐的角∠B是150°,第三次拐的角是∠C,这时的道路恰好和第一次拐弯之前的道路平行,则∠C是( )
如图,一条公路修到湖边时,需拐弯绕道而过,如果第一次拐的角∠A是100°第二次拐的角∠B是150°,第三次拐的角是∠C,这时的道路恰好和第一次拐弯之前的道路平行,则∠C是( )| A. | 120° | B. | 130° | C. | 140° | D. | 150° |
1.在△ABC中,∠A:∠B:∠C=1:2:3,AB=a,则CB等于( )
| A. | $\frac{a}{2}$ | B. | $\frac{a}{3}$ | C. | $\frac{a}{4}$ | D. | 以上结果都不对 |
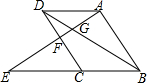 如图,?ABCD,点E是BC延长线上一点,连接AE,分别交BD、CD于点G、F,若AG=2,GF=1,则EF=3.
如图,?ABCD,点E是BC延长线上一点,连接AE,分别交BD、CD于点G、F,若AG=2,GF=1,则EF=3.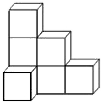 如图所示的几何体是由7个相同的小正方体搭成的,请画出这个图形的主视图、左视图和俯视图.
如图所示的几何体是由7个相同的小正方体搭成的,请画出这个图形的主视图、左视图和俯视图. 如图为一次函数y=kx+b的图象,则一次函数y=bx+k的图象大致是( )
如图为一次函数y=kx+b的图象,则一次函数y=bx+k的图象大致是( )

