题目内容
7.已知函数y=(k+2)x2+2x-k的图象与坐标轴有两个交点,则k的值是-1或-2或0.分析 当k+2=0时,为一次函数,则与x轴和y轴各有一个交点满足条件;当k+2≠0时,则根据对应一元二次方程的判别式为可求得k的值;当二次函数过原点时也满足条件,可求得k的值.
解答 解:
当k+2=0时,即k=-2,函数y=x+2,与x轴和y轴各有一个交点,满足条件;
当k+2≠0时,由函数与y轴交于点(0,-k),-k=0,k=0,
则与x轴只能有一个交点,
∴△=22+4k(k+2)=0,解得k=-1;
综上可知k的值为-1或-2或0,
故答案为:-1或-2或0.
点评 本题主要考查二次函数与坐标轴的交点,掌握二次函数的交点个数与对应一元二次方程根的个数的关系是解题的关键,注意分类讨论.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 完成下面推理过程:
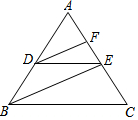
完成下面推理过程: 如图,在△ABC中,AD⊥BC,AE平分∠BAC,∠B=50°,∠C=30°,则∠DAE=10°.
如图,在△ABC中,AD⊥BC,AE平分∠BAC,∠B=50°,∠C=30°,则∠DAE=10°. 如图,说出数轴上点A所表示的数是-$\sqrt{5}$.
如图,说出数轴上点A所表示的数是-$\sqrt{5}$.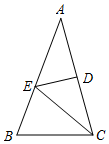 如图,△ABC中,∠A=36°,AC的垂直平分线交AB于E,D为垂足,AB=AC,连结EC.
如图,△ABC中,∠A=36°,AC的垂直平分线交AB于E,D为垂足,AB=AC,连结EC.