题目内容
16．
如图，说出数轴上点A所表示的数是-$\sqrt{5}$．
分析 先根据勾股定理求出斜边的长度，再根据点A在数轴上的位置即可求解．
解答 解：由勾股定理，得斜边的长为：$\sqrt{{2}^{2}+{1}^{2}}$=$\sqrt{5}$，
则数轴上点A所表示的数是-$\sqrt{5}$．
故答案为-$\sqrt{5}$．
点评 本题考查了实数与数轴，勾股定理，求出斜边的长度是解题的关键．
练习册系列答案
相关题目
11．已知一次函数y=kx+k，若y随x的增大而增大，则它的图象经过（ ）
| A． | 第一、二、三象限 | B． | 第一、三、四象限 | C． | 第一、二、四象限 | D． | 第二、三、四象限 |
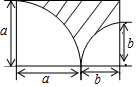在如图所示的长方形中，请用含字母a，b的代数式表示阴影面积，并按字母a降幂排列得（1-$\frac{1}{4}$π）a2+ab-$\frac{1}{4}$πb2．