题目内容
20.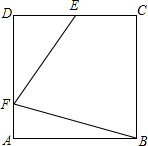 如图,在正方形ABCD中,E、F分别是CD、AD上的一点,连接BF、FE,DE=CE,且∠BFE=∠FBC
如图,在正方形ABCD中,E、F分别是CD、AD上的一点,连接BF、FE,DE=CE,且∠BFE=∠FBC(1)直接写出∠DEF+∠DFE的值90°;
(2)求:$\frac{AF}{AB}$的值.
分析 (1)根据正方形的性质,∠D=90°,即△DEF为直角三角形,所以∠DEF+∠DFE=90°;
(2)延长BC,FE交于点P,构造等腰三角形PEB,利用正方形的性质和中点的性质求得PB的长后,由勾股定理求得a的值.则可求出AB,AF的值.
解答 (1)∵四边形ABCD为正方形,
∴∠D=90°,即△DEF为直角三角形,
∴∠DEF+∠DFE=90°,
故答案为:90°;
(2)如图,延长BC,FE交于点P,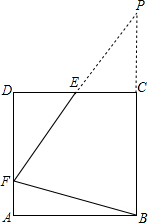
∵正方形ABCD,
∴AD∥BC.
∴△DEF∽△CEP.
∵E为CD的中点,
∴$\frac{EF}{EP}=\frac{DE}{CE}$=1,PF=2EF.
∵∠BFE=∠FBC,
∴PB=PF.
设AF=a,
∴PC=DF=4-a,PB=PF=8-a,
EF=$\frac{PF}{2}=\frac{8-a}{2}$.AB=(8-a)-(4-a)=4,
∵Rt△DEF中,EF2=DE2+DF2,
∴$(\frac{8-a}{2})^{2}$=22+(4-a)2整理,得3a2-16a+16=0,
解得,a1=$\frac{4}{3}$,a2=4;
∵F点不与D点重合,
∴a=4不成立,a=$\frac{4}{3}$,
∴$\frac{AF}{AB}=\frac{\frac{4}{3}}{4}=\frac{1}{3}$.
点评 本题利用了正方形的性质,中点的性质,等腰三角形的性质,勾股定理求解,解决本题的关键是作出辅助线.

练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案
相关题目
 如图,雷达可用于飞机导航,也可用来监测飞机的飞行.假设某时刻雷达向飞机发射电磁波,电磁波遇到飞机后反射,又被雷达接收,两个过程共用了5.24×10-5秒.已知电磁波的传播速度为3.0×108米/秒,则该时刻飞机与雷达站的距离是7.86×103米.
如图,雷达可用于飞机导航,也可用来监测飞机的飞行.假设某时刻雷达向飞机发射电磁波,电磁波遇到飞机后反射,又被雷达接收,两个过程共用了5.24×10-5秒.已知电磁波的传播速度为3.0×108米/秒,则该时刻飞机与雷达站的距离是7.86×103米. 如图是一个数值运算程序,当输出的数为18时,输入的数为7或34.
如图是一个数值运算程序,当输出的数为18时,输入的数为7或34.
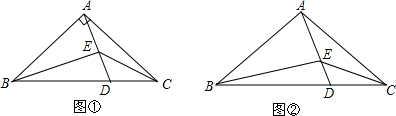
 如图,已知Rt△ABC≌Rt△ADE,∠ABC=∠ADE=90°,BC与DE相交于点F,连接CD,EB.求证:
如图,已知Rt△ABC≌Rt△ADE,∠ABC=∠ADE=90°,BC与DE相交于点F,连接CD,EB.求证: