题目内容
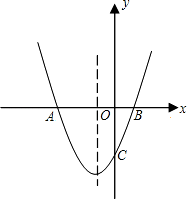
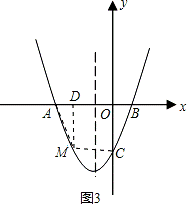
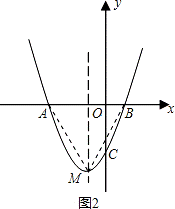
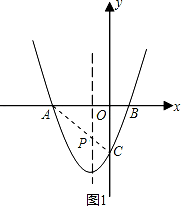
如图,抛物线y=(x+1)2+k与x轴交于A、B两点,与y轴交于点C(0,﹣3)
(1)求抛物线的对称轴及k的值;
(2)抛物线的对称轴上存在一点P,使得PA+PC的值最小,求此时点P的坐标;
(3)点M是抛物线上的一动点,且在第三象限.
①当M点运动到何处时,△AMB的面积最大?求出△AMB的最大面积及此时点M的坐标;
②当M点运动到何处时,四边形AMCB的面积最大?求出四边形AMCB的最大面积及此时点的坐标.
解:(1)∵抛物线y=(x+1)2+k与y轴交于点C(0,﹣3),
∴﹣3=1+k,
∴k=﹣4,
∴抛物线的解析式为:y=(x+1)2﹣4,
∴抛物线的对称轴为:直线x=﹣1;
(2)存在.
连接AC交抛物线的对称轴于点P,则PA+PC的值最小,
当y=0时,(x+1)2﹣4=0,
解得:x=﹣3或x=1,
∵A在B的左侧,
∴A(﹣3,0),B(1,0),
设直线AC的解析式为:y=kx+b,
∴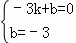 ,
,
解得: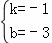 ,
,
∴直线AC的解析式为:y=﹣x﹣3,
当x=﹣1时,y=﹣(﹣1)﹣3=﹣2,
∴点P的坐标为:(﹣1,﹣2);
(3)点M是抛物线上的一动点,且在第三象限,
∴﹣3<x<0;
①设点M的坐标为:(x,(x+1)2﹣4),
∵AB=4,
∴S△AMB=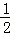 ×4×|(x+1)2﹣4|=2|(x+1)2﹣4|,
×4×|(x+1)2﹣4|=2|(x+1)2﹣4|,
∵点M在第三象限,
∴S△AMB=8﹣2(x+1)2,
∴当x=﹣1时,
即点M的坐标为(﹣1,﹣4)时,△AMB的面积最大,最大值为8;
②设点M的坐标为:(x,(x+1)2﹣4),
过点M作MD⊥AB于D,
S四边形ABCM=S△OBC+S△ADM+S梯形OCMD=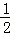 ×3×1+
×3×1+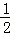 ×(3+x)×[4﹣(x+1)2]+
×(3+x)×[4﹣(x+1)2]+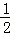 ×(﹣x)×[3+4﹣(x+1)2]
×(﹣x)×[3+4﹣(x+1)2]
=﹣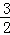 (x2+3x﹣4)=﹣
(x2+3x﹣4)=﹣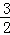 (x+
(x+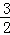 )2+
)2+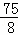 ,
,
∴当x=﹣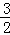 时,y=(﹣
时,y=(﹣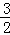 +1)2﹣4=﹣
+1)2﹣4=﹣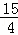 ,
,
即当点M的坐标为(﹣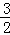 ,﹣
,﹣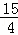 )时,四边形AMCB的面积最大,最大值为
)时,四边形AMCB的面积最大,最大值为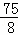 .
.

甲、乙、丙、丁四名射击运动员参加射击预选赛,他们射击 成绩的平均环数
成绩的平均环数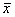 及方差
及方差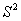 如下表所示:
如下表所示:
| 甲 | 乙 | 丙 | 丁 | |
|
|
|
|
|
|
|
| 1 | 1.1 |
|
|
若要选出一个成绩较好且状态稳定的运动员去参赛,那么应选运动员( )
A.甲 B.乙 C.丙 D.丁
 h(cm)
h(cm) 20
20