题目内容
在平面直角坐标系中,O为坐标原点,点A坐标为(1,0),以OA 为边在第一象限内作等边△OAB,C为x轴正半轴上的一个动点(OC>1),连接BC,以BC为边在第一象限内作等边△BCD,直线DA交y轴于E点.
为边在第一象限内作等边△OAB,C为x轴正半轴上的一个动点(OC>1),连接BC,以BC为边在第一象限内作等边△BCD,直线DA交y轴于E点.
(1)如图,当C点在x轴上运动时,设AC=x,请用x表示线段AD的长;
(2)随着C点的变化,直线AE的位置变化吗?若变化,请说明理由;若不变,请求出直线AE的解析式.
(3)以线段BC为直径作圆,圆心为点F,
①当C点运动到何处时直线EF∥直线BO?此时⊙F和直线BO的位置关系如何?请说明理由.
②G为CD与⊙F的交点,H为直线DF上的一个动点 ,连结HG、HC,求HG+HC的最小值,并将此最小值用x表示.
,连结HG、HC,求HG+HC的最小值,并将此最小值用x表示.
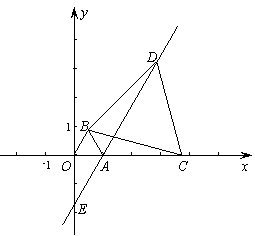
解:(1)∵△OAB和△BCD都为等边三角形,∴OB=AB,BC=BD,∠OBA=∠DBC=60°,即∠OBA+∠ABC=∠DBC+∠ABC,∴∠OBC=∠ABD,∴△OBC≌△ABD,∴AD=OC=1+x;
(2)随着C点的变化,直线AE的位置不变.理由如下:
由△OBC≌△ABD,得到∠BAD=∠BOC=60°,又∵∠BAO=60°,∴∠DAC=60°,
∴∠OAE=60°,又OA=1,
在直角三角形AOE中, OE= ,点E坐标为(0,﹣
,点E坐标为(0,﹣ ),A(1,0),
),A(1,0),
设直线AE解析式为y=kx+b,把E和A的坐标代入得: ,
,
解得: ,
,
所以直线AE的解析式为y= x﹣
x﹣ ;
;
(3)根据题意画出图形,如图所示:∵∠BOA=∠DAC=60°,EA∥OB,又EF∥OB,
则EF与EA所在的直线重合,∴点F为DE与BC的交点,又F为BC中点,∴A为OC中点,又AO=1,则OC=2,∴当C的坐标为(2,0)时,EF∥OB;这时直线BO与⊙F相切,理由如下:
∵△BCD为等边三角形,F为BC中点,∴DF⊥BC,又EF∥OB,∴FB⊥OB,即∠FBO=90°,
故直线BO与⊙F相切;
|
|

 阅读快车系列答案
阅读快车系列答案
 b、c满足a2+b2+c2+338=10a+24b+26c,则此△为等腰直角三角形。
b、c满足a2+b2+c2+338=10a+24b+26c,则此△为等腰直角三角形。 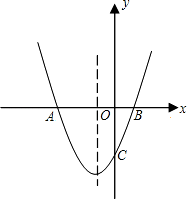

 ,可知( )
,可知( )
 时,
时,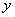 随
随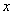 的增大而增大
的增大而增大
 ∠B=∠D B.AB∥CD AD=BC C.AB∥CD ∠A=∠C D.AB∥CD AB=CD
∠B=∠D B.AB∥CD AD=BC C.AB∥CD ∠A=∠C D.AB∥CD AB=CD  ,其中
,其中 .
.