Question

如图，利用一面墙（墙的长度不超过45m），用80m长的篱笆围一个矩形场地．

（1）怎样围才能使矩形场地的面积为750m²？

（2）能否使所围矩形场地的面积为810m²，为什么？

Answer 1

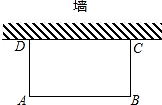
解：（1）设所围矩形ABCD的长AB为x米，则宽AD为（80﹣x）米（1分）．

（说明：AD的表达式不写不扣分）．

依题意，得x•（80﹣x）=750（2分）．

即，x²﹣80x+1500=0，

解此方程，得x₁=30，x₂=50．

∵墙的长度不超过45m，∴x₂=50不合题意，应舍去（4分）．

当x=30时，（80﹣x）=×（80﹣30）=25，

所以，当所围矩形的长为30m、宽为25m时，能使矩形的面积为750m²（5分）．

（2）不能．

因为由x•（80﹣x）=810得x²﹣80x+1620=0（6分）．

又∵b²﹣4ac=（﹣80）²﹣4×1×1620=﹣80＜0，

∴上述方程没有实数根（7分）．

因此，不能使所围矩形场地的面积为810m²（8分）．

说明：如果未知数的设法不同，或用二次函数的知识解答，只要过程及结果正确，请参照给分．