题目内容
 如图,已知AB是直径,弦CD与AB相交于点P,且将AB分成2和8两段,∠DPB=30°,求弦CD的长.
如图,已知AB是直径,弦CD与AB相交于点P,且将AB分成2和8两段,∠DPB=30°,求弦CD的长.考点:垂径定理,含30度角的直角三角形,勾股定理
专题:
分析:过点O作OE⊥CD于点E,连接OD,先根据弦CD与AB相交于点P,且将AB分成2和8两段得出⊙O的半径及OP的长,再根据∠DPB=30°求出OE的长,再根据勾股定理求出DE的长,进而可得出结论.
解答: 解:过点O作OE⊥CD于点E,连接OD,
解:过点O作OE⊥CD于点E,连接OD,
∵弦CD与AB相交于点P,且将AB分成2和8两段,
∴⊙O的半径=5,OP=5-2=3.
∵∠DPB=30°,
∴OE=
OP=
.
∵OD=5,
∴DE=
=
=
,
∴CD=2DE=9.
 解:过点O作OE⊥CD于点E,连接OD,
解:过点O作OE⊥CD于点E,连接OD,∵弦CD与AB相交于点P,且将AB分成2和8两段,
∴⊙O的半径=5,OP=5-2=3.
∵∠DPB=30°,
∴OE=
| 1 |
| 2 |
| 3 |
| 2 |
∵OD=5,
∴DE=
| OD2-OE2 |
52-(
|
| 9 |
| 2 |
∴CD=2DE=9.
点评:本题考查的是垂径定理,根据题意作出辅助线,构造出直角三角形是解答此题的关键.

练习册系列答案
相关题目
 如图,将方格纸中的图形绕点O逆时针旋转90°后得到的图形是( )
如图,将方格纸中的图形绕点O逆时针旋转90°后得到的图形是( )A、 |
B、 |
C、 |
D、 |
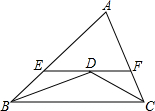 如图,在△ABC中,BD、CD分别平分∠ABC、∠ACB,过点D作直线平行于BC,交AB、AC于点E、F,当∠A的位置及大小变化时,线段EF和BE+CF的大小关系为( )
如图,在△ABC中,BD、CD分别平分∠ABC、∠ACB,过点D作直线平行于BC,交AB、AC于点E、F,当∠A的位置及大小变化时,线段EF和BE+CF的大小关系为( )| A、EF>BE+CF |
| B、EF=BE+CF |
| C、EF<BE+CF |
| D、不能确定 |
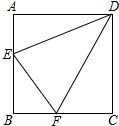 在正方形ABCD中,∠EDF=45°,求证:EF=AE+CF.
在正方形ABCD中,∠EDF=45°,求证:EF=AE+CF. 如图,Rt△ABC的硬纸片,∠BAC=90°,AB=3,BC=5,AD为BC边上的高,从这张硬纸片剪下一个如图所示的内接正方形EFGH,则正方形EFGH的边长为
如图,Rt△ABC的硬纸片,∠BAC=90°,AB=3,BC=5,AD为BC边上的高,从这张硬纸片剪下一个如图所示的内接正方形EFGH,则正方形EFGH的边长为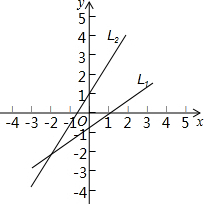 图中两直线L1,L2的交点坐标可以看作是方程组
图中两直线L1,L2的交点坐标可以看作是方程组