题目内容
14.如图,△ABC是等腰直角三角形,动点P在斜边AB所在的射线上,以PC为直角边作等腰直角三角形PCQ,已知∠PCQ=90°,设∠ACP=α.(1)则图中∠BCQ=α(用含α的代数式表示);
(2)探究:
①由操作知,动点P在射线AB的不同位置时,α的大小不同,直接写出α的取值范围;
②若△PCQ的面积最小,求α的值;
③若△BPC是等腰三角形,求α的值.
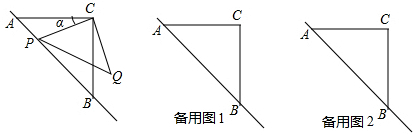
分析 (1)根据同角的余角相等进行判断即可;
(2)①分四种情况讨论:当点P与点A重合时;当点P在AB之间(不与A、B重合)时;当点P与点B重合时;当点P在AB的延长线上时,分别求得α的取值范围;
②根据垂线段最短可得,当CP⊥AB时,CP最短,此时,等腰Rt△PCQ的面积最小,求得α=45°;
③分四种情况讨论,分别根据三角形内角和定理以及等腰直角三角形的性质,求得α的值.
解答 解:(1)∵△ABC是等腰直角三角形,∠PCQ=90°,
∴∠ACB=∠PCQ=90°,
∴∠ACB-∠PCB=∠PCQ-∠PCB,
∴∠ACP=∠BCQ=α,
故答案为:α;
(2)①当点P与点A重合时,∠ACP=α=0°;
当点P在AB之间(不与A、B重合)时,∠ACP为锐角,即0°<α<90°;
当点P与点B重合时,∠ACP为直角,即α=90°;
当点P在AB的延长线上时,∠ACP是钝角,90°<α<135°;
②根据垂线段最短可得,当CP⊥AB时,CP最短,如图所示,
此时,等腰Rt△PCQ的面积最小,
∴α=∠CPB-∠BAC=90°-45°=45°;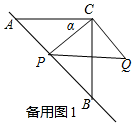
③如图所示,当CA=CB时,△BCP是等腰直角三角形,此时点P与点A重合,∠ACP=α=0°;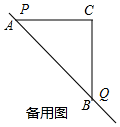
如图所示,当BC=BP时,△BCP是等腰三角形,此时∠BCP=$\frac{180°-45°}{2}$=67.5°,
∴∠ACP=α=90°-67.5°=22.5°;
如图所示,当PB=PC时,△BCP是等腰直角三角形,此时∠PCB=45°,
∴∠ACP=α=90-45°=45°;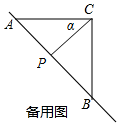
如图所示,当BP=BC时,△BCP是等腰三角形,此时∠BCP=$\frac{45°}{2}$=22.5°,
∴∠ACP=α=90°+22.5°=112.5°;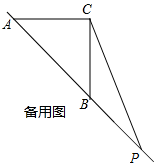
综上所述,α的值为0°,22.5°,45°,112.5°.
点评 本题属于三角形综合题,主要考查了等腰三角形的判定与性质、等腰直角三角形的性质以及三角形内角和定理的综合应用,解决问题的关键是掌握:三角形的内角和等于180°,解题时注意分类讨论思想和垂线段最短的运用,分类时不能重复,也不能遗漏.

 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案 如图,已知DE∥AB,EF∥BC,且OD:DA=3:2,则△ABC与△DEF是位似图形,位似比为3:5;△OAB与△OED是位似图形,位似中心是点O.
如图,已知DE∥AB,EF∥BC,且OD:DA=3:2,则△ABC与△DEF是位似图形,位似比为3:5;△OAB与△OED是位似图形,位似中心是点O. 如图,△ABC≌△FED,AC与DF是对应边,∠C与∠D是对应角,则AC∥FD成立吗?请说明理由.
如图,△ABC≌△FED,AC与DF是对应边,∠C与∠D是对应角,则AC∥FD成立吗?请说明理由.