题目内容
19.一条河上有甲、乙两个码头,甲码头在乙码头的上游50千米处,一艘客船和一艘货船分别从甲、乙两码头同时出发向上游行驶,两船的静水速度相同,客船出发时有一物品从船上落入水中,10分钟后此物品距客船5千米,客船在行驶20千米后掉头追赶此物品,追上时恰好和货船相遇,求水流的速度.分析 设水流的速度为x千米/时,两船的静水速度为a千米/时,设物品和货船相遇时间为t小时,由题意得:$\frac{10}{60}$(a-x+x)=5,解得a=30千米/时,因为物品和货船相遇时间t(x+a-x)=50,t=$\frac{5}{3}$小时,因为两船的静水速度相同,所以当客船行20千米时,货船也行20千米,两船之间的距离还是50千米,推出客船从20千米处回头和货船的相遇时间:50÷(30×2)=$\frac{5}{6}$(小时),推出所以客船逆流行驶20千米的时间为$\frac{5}{3}$-$\frac{5}{6}$=$\frac{5}{6}$小时,可得方程$\frac{5}{6}$(30-x)=20,解方程即可.
解答 解:设水流的速度为x千米/时,两船的静水速度为a千米/时,设物品和货船相遇时间为t小时,
由题意得:$\frac{10}{60}$(a-x+x)=5,解得a=30千米/时,
物品和货船相遇时间t(x+a-x)=50,t=$\frac{5}{3}$小时,
因为两船的静水速度相同,所以当客船行20千米时,货船也行20千米,两船之间的距离还是50千米,
客船从20千米处回头和货船的相遇时间:50÷(30×2)=$\frac{5}{6}$(小时),
所以客船逆流行驶20千米的时间为$\frac{5}{3}$-$\frac{5}{6}$=$\frac{5}{6}$小时,
所以$\frac{5}{6}$(30-x)=20,
解得x=6千米/时.
答:水流的速度为6千米/时.
点评 此题主要考查了一元一次方程的应用,关键是正确理解题意,找出题目中的等量关系,列出方程,常用的等量关系:相遇时间×速度和=相遇距离;追击时间×速度差=追击距离,所以中考常考题型.

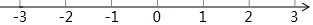 把75%,2的相反数,$-2\frac{1}{3}$,-(-3),-12各数所表示的点在数轴上分别用字母“A、B、C、D、E”标出来,再用“<”把这些数连接起来.
把75%,2的相反数,$-2\frac{1}{3}$,-(-3),-12各数所表示的点在数轴上分别用字母“A、B、C、D、E”标出来,再用“<”把这些数连接起来.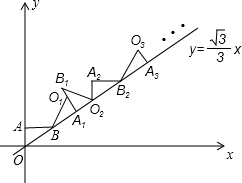 如图,A(0,1),B($\sqrt{3}$,1),将△ABO绕点B旋转到△A1B1O1的位置,点A的对应点A1落在直线y=$\frac{\sqrt{3}}{3}$x上,再将△A1BO1绕点A1旋转到△A2B1O2的位置,点O1的对应点O2也落在直线上,依次下去…,若点则点B8坐标是(6+7$\sqrt{3}$,7+2$\sqrt{3}$).
如图,A(0,1),B($\sqrt{3}$,1),将△ABO绕点B旋转到△A1B1O1的位置,点A的对应点A1落在直线y=$\frac{\sqrt{3}}{3}$x上,再将△A1BO1绕点A1旋转到△A2B1O2的位置,点O1的对应点O2也落在直线上,依次下去…,若点则点B8坐标是(6+7$\sqrt{3}$,7+2$\sqrt{3}$).
 如图,在矩形OABC中,OA=3,OC=2,F是AB上的一个动点(F不与A,B重合),过点F的反比例函数y=$\frac{k}{x}$(x>0)的图象与BC边交于点E.
如图,在矩形OABC中,OA=3,OC=2,F是AB上的一个动点(F不与A,B重合),过点F的反比例函数y=$\frac{k}{x}$(x>0)的图象与BC边交于点E.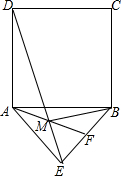 如图,正方形ABCD中,AB=8,以AB为斜边向下作等腰Rt△ABE,F为EB的中点,连接DE、AF交于点M,连接BM,则BM的长为$\sqrt{26}$.
如图,正方形ABCD中,AB=8,以AB为斜边向下作等腰Rt△ABE,F为EB的中点,连接DE、AF交于点M,连接BM,则BM的长为$\sqrt{26}$.