题目内容
9. 如图,已知DE∥AB,EF∥BC,且OD:DA=3:2,则△ABC与△DEF是位似图形,位似比为3:5;△OAB与△OED是位似图形,位似中心是点O.
如图,已知DE∥AB,EF∥BC,且OD:DA=3:2,则△ABC与△DEF是位似图形,位似比为3:5;△OAB与△OED是位似图形,位似中心是点O.
分析 根据位似图形的定义:对应顶点的连线相交于一点,对应边互相平行,即可解决.
解答 解: ∵DE∥AB,EF∥BC,
∵DE∥AB,EF∥BC,
∴$\frac{OD}{OA}$=$\frac{OE}{OB}$,$\frac{OE}{OB}$=$\frac{OF}{OC}$,
∴$\frac{OD}{OA}$=$\frac{OF}{OC}$,
∴DF∥AC,
∵△ABC与△DEF的对应顶点交于点O,
∴△ABC与△DEF是位似图形,位似比=3:5,同理△OAB与△ODE是位似图形,位似中心是点O.
故答案为△DEF,3:5,△ODE,O.
点评 本题考查位似图形的定义,记住对应顶点的连线相交于一点,对应边互相平行的两个三角形是位似图形,属于基础题,中考常考题型.

练习册系列答案
 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
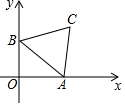 如图,点A,B分别是x轴.y轴上的两个动点,以AB为边作等边△ABC,若AB=2,设点C到原点O的距离为d,则d的取值范围是$\sqrt{3}$-1≤d≤$\sqrt{3}$+1.
如图,点A,B分别是x轴.y轴上的两个动点,以AB为边作等边△ABC,若AB=2,设点C到原点O的距离为d,则d的取值范围是$\sqrt{3}$-1≤d≤$\sqrt{3}$+1.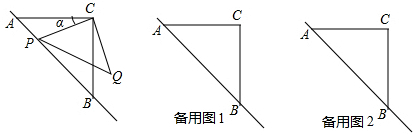
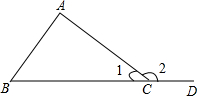 已知:如图,∠2是△ABC的一个外角.求证:∠2=∠A+∠B
已知:如图,∠2是△ABC的一个外角.求证:∠2=∠A+∠B