题目内容

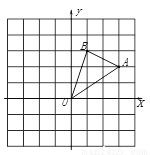
如图，在边长为1的正方形组成的网格中建立直角坐标系，△AOB的顶点均在格点上，点O为原点，点A、B的的坐标分别为A（3，2）、B（1，3）.

⑴.请画出将△AOB向左平移3个单位后得到的图形△A1OB1，点B1的坐标为 ；

⑵.请画出将△AOB关于原点O成对称的图形△A2OB2，点A2的坐标为 ；

⑶.在x轴上找一点P，使PA+PB的值最小，则P点的坐标为 .

(1)作图见解析，B1（-2，3）；（2）作图见解析，A2(-3,-2);(3)作图见解析，P(2.2,0). 【解析】试题分析：（1）根据平移规律解答； （2）根据中心对称图形的概念解答； （3）根据轴对称-最短路径问题解答． 试题解析：（1）将△AOB向左平移3个单位后得到的图形△A1OB1如图所示， 点B1的坐标为（-2，3）； （2）将△AOB关于原点O...
练习册系列答案
相关题目

已知点P的坐标是（2，﹣3），那么点P关于原点的对称点P1的坐标是_____．

（2，﹣3） 【解析】试题解析：∵点P的坐标是（2，﹣3）， ∴点P关于原点的对称点P1的坐标是（﹣2，3）． 故答案为：（﹣2，3），

在一节数学实践活动课上，老师拿出三个边长都为5cm的正方形硬纸板，他向同学们提出了这样一个问题：若将三个正方形纸板不重叠地放在桌面上，用一个圆形硬纸板将其盖住，这样的圆形硬纸板的最小直径应有多大？问题提出后，同学们经过讨论，大家觉得本题实际上就是求将三个正方形硬纸板无重叠地适当放置，圆形硬纸板能盖住时的最小直径．老师将同学们讨论过程中探索出的三种不同摆放类型的图形画在黑板上，如下图所示：

（1）计算（结果保留根号与π）．

（Ⅰ）图①能盖住三个正方形所需的圆形硬纸板最小直径应为 cm；

（Ⅱ）图②能盖住三个正方形所需的圆形硬纸板最小直径为 cm；

（Ⅲ）图③能盖住三个正方形所需的圆形硬纸板最小直径为 cm；

（2）其实上面三种放置方法所需的圆形硬纸板的直径都不是最小的，请你画出用圆形硬纸板盖住三个正方形时直径最小的放置方法，（只要画出示意图，不要求说明理由），并求出此时圆形硬纸板的直径．

（1）（Ⅰ）5cm；（Ⅱ）10cm；（Ⅲ）10cm；（2）直径为. 【解析】试题分析：（1）（Ⅰ）观察图形可知：图①能盖住三个正方形所需的圆形硬纸板最小直径=三个正方形组成的矩形的对角线长，利用勾股定理可求出结果；（Ⅱ）图②中圆形硬纸板的半径是正方形的对角线长，利用勾股定理可求出结果；（Ⅲ）图③中圆形硬纸板的直径是正方形的对角线长的2倍，利用勾股定理可求出结果；（2）把三个正方形摆成“品”字...

已知抛物线y=ax2+bx和直线y=ax+b在同一坐标系内的图象如图，其中正确的是 （　　）

A. B.

C. D.

D 【解析】试题分析：选项A、由二次函数的图象可知a＜0，此时直线y=ax+b经过二、四象限，故A可排除；选项B、二次函数的图象可知a＜0，对称轴在y轴的右侧，可知a、b异号，b＞0，此时直线y=ax+b经过一、二、四象限，故B可排除；选项C、二次函数的图象可知a＞0，此时直线y=ax+b经过一、三，故C可排除；正确的只有D．故答案选D．

在Rt△ABC中，∠A=90°，AC=AB=4，D，E分别是边AB，AC的中点，若等腰Rt△ADE绕点A逆时针旋转，得到等腰Rt△AD1E1，设旋转角为α（0＜α≤180°），记直线BD1与CE1的交点为P．

（1）如图1，当α=90°时，线段BD1的长等于　　　　　　，线段CE1的长等于　　　　　　；（直接填写结果）

（2）如图2，当α=135°时，求证：BD1=CE1，且BD1⊥CE1.

（1）2； 2；（2）证明见解析. 【解析】试题分析：（1）利用等腰直角三角形的性质结合勾股定理分别得出BD1的长和CE1的长； （2）根据旋转的性质得出，∠D1AB=∠E1AC=135°，进而求出△D1AB≌△E1AC（SAS），即可得出答案. 试题解析：（1）∵∠A=90°，AC=AB=4，D，E分别是边AB，AC的中点， ∴AE=AD=2， ∵等腰Rt△ADE绕...

如图，△ABC中，AB=4，AC=2，BC=2，以BC为直径的半圆交AB于点D，以A为圆心，AC为半径的扇形交AB于点E．则图中阴影部分的面积_______________

【解析】试题解析：∵Rt△ABC中，cosA=． ∴∠A=60°． ∴S阴影=S半圆-（S△ABC-S扇形ACE） =π（）2-（×2×2-π×22） =.

已知点和关于原点对称，则的值为（ ）

A. 1 B. 0 C. -1 D.

A 【解析】试题解析：根据题意得：a-1=-2，b-1=-1， 解得：a=-1 b=0． 则（a+b）2008=1． 故选A．

如图，按照程序图计算，当输入正整数时，输出的结果是，则输入的的值可能是__________．

、、、． 【解析】【解析】 ∵y=3x+2，如果直接输出结果，则3x+2=161，解得：x=53； 如果两次才输出结果：则x=(53-2)÷3=17； 如果三次才输出结果：则x=(17-2)÷3=5； 如果四次才输出结果：则x=(5-2)÷3=1； 则满足条件的整数值是：53、17、5、1． 故答案为：53、17、5、1．

已知多项式A、B,其中A=x2-2x+1,小马在计算A+B时,由于粗心把A+B看成了A-B求得结果为-3x2-2x-1,请你帮小马算出A+B的正确结果.

5x2-2x+3 【解析】试题分析：根据的差，求出，即可确定出 试题解析： 根据题意得： 则

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网