题目内容
4. 已知:△ABC在直角坐标平面内,三个顶点的坐标分别为A(1,0)、
已知:△ABC在直角坐标平面内,三个顶点的坐标分别为A(1,0)、B(3,2)、C(0,1)(正方形网格中每个小正方形的边长是一个单位长度).
(1)沿x轴向左平移2个单位,得到△A1B1C1,不画图直接写出发生变化后的B1点的坐标.点B1的坐标是(1,2);
(2)以A点为位似中心,在网格内画出△A2B2C2,使△A2B2C2与△ABC位似,且位似比为2:1,则点B2的坐标是(-3,-4);
(3)△A2B2C2的面积是8平方单位.
分析 (1)直接利用平移的性质,得出各对应点位置进而得出答案;
(2)利用位似图形的性质,得出对应点位置进而得出答案;
(3)直接利用割补法,求得△A2B2C2面积即可,将该三角形看成上下两部分即可得出答案.
解答 解:(1)根据平移规律,将点B(3,2)左平移2个单位,得到点B1的坐标是(1,2),
故答案为:(1,2);
(2)如图所示,△A2B2C2即为所求,B2(-3,-4);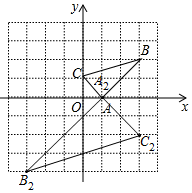
故答案为:(-3,-4);
(3)△A2B2C2的面积是:$\frac{1}{2}$×4×2+$\frac{1}{2}$×4×2=8.
故答案为:8.
点评 此题主要考查了位似变换以及平移变换和三角形面积求法等知识,根据题意得出对应点位置是解题关键.解题时注意:在计算三角形面积时可以运用割补法.

练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目
16.李华骑自行车到学校,若每小时骑15km,则早到10分钟;若每小时骑12km,则迟到2分钟,请问他家到学校的路程是多少km?设他家到学校的路程是xkm,则根据题意列出方程是( )
| A. | $\frac{x}{15}$-$\frac{10}{60}$=$\frac{x}{12}$+$\frac{2}{60}$ | B. | $\frac{x}{15}$+$\frac{10}{60}$=$\frac{x}{12}$-$\frac{2}{60}$ | ||
| C. | $\frac{x}{15}$+10=$\frac{x}{12}$-2 | D. | $\frac{x}{15}$-10=$\frac{x}{12}$+2 |
14.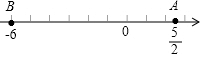 在数轴上A,B两点表示的数如图所示,则A、B两点间的距离是( )
在数轴上A,B两点表示的数如图所示,则A、B两点间的距离是( )
 在数轴上A,B两点表示的数如图所示,则A、B两点间的距离是( )
在数轴上A,B两点表示的数如图所示,则A、B两点间的距离是( )| A. | $\frac{5}{2}$ | B. | $\frac{17}{2}$ | C. | $\frac{11}{2}$ | D. | 6 |
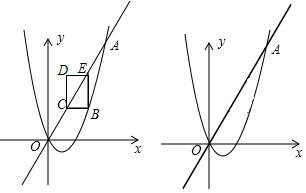
 如图,已知∠ACB=∠DCE=90°,AC=BC,CD=CE,试说明BE与AD的数量与位置关系.
如图,已知∠ACB=∠DCE=90°,AC=BC,CD=CE,试说明BE与AD的数量与位置关系.
 如图,A(-4,$\frac{1}{2}$)、B(-1,2)是反比例函数y=$\frac{a}{x}$与一次函数y=kx+b的图象在第二象限内的两个交点,AM⊥x轴于M,BN⊥y轴于N,
如图,A(-4,$\frac{1}{2}$)、B(-1,2)是反比例函数y=$\frac{a}{x}$与一次函数y=kx+b的图象在第二象限内的两个交点,AM⊥x轴于M,BN⊥y轴于N,