题目内容
7. 如图所示,在一张长为8cm,宽为6cm的矩形纸片上,现要剪下一个腰长为5cm的等腰三角形(要求:等腰三角形的一个顶点与矩形的一个顶点重合,其余的两个顶点在矩形的边上),则剪下的等腰三角形的面积为①、③、⑤(把下列正确序号填在横线上).
如图所示,在一张长为8cm,宽为6cm的矩形纸片上,现要剪下一个腰长为5cm的等腰三角形(要求:等腰三角形的一个顶点与矩形的一个顶点重合,其余的两个顶点在矩形的边上),则剪下的等腰三角形的面积为①、③、⑤(把下列正确序号填在横线上).①$\frac{25}{2}$cm2;②6cm2;③10cm2;④12cm2;⑤5$\sqrt{6}$cm2.
分析 因为等腰三角形腰的位置不明确,所以分(1)腰长在矩形相邻的两边上,(2)一腰在矩形的宽上,(3)一腰在矩形的长上,三种情况讨论.(1)△AEF为等腰直角三角形,直接利用面积公式求解即可;(2)先利用勾股定理求出AE边上的高BF,再代入面积公式求解;(3)先求出AE边上的高DF,再代入面积公式求解.
解答 解:分三种情况计算:
(1)当AE=AF=5厘米时,
∴S△AEF=$\frac{1}{2}$AE•AF=$\frac{1}{2}$×5×5=$\frac{25}{2}$厘米2;
(2)当AE=EF=5厘米时,如图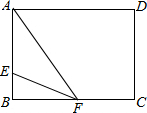
BF=$\sqrt{E{F}^{2}-B{E}^{2}}$=$\sqrt{{5}^{2}-{1}^{2}}$=2$\sqrt{6}$厘米,
∴S△AEF=$\frac{1}{2}$•AE•BF=$\frac{1}{2}$×5×2$\sqrt{6}$=5$\sqrt{6}$厘米2;
(3)当AE=EF=5厘米时,如图
DF=$\sqrt{E{F}^{2}-D{E}^{2}}$=$\sqrt{{5}^{2}-{3}^{2}}$=4厘米,
∴S△AEF=$\frac{1}{2}$AE•DF=$\frac{1}{2}$×5×4=10厘米2.
综上所述,剪下的等腰三角形的面积为:$\frac{25}{2}$、5$\sqrt{6}$、10.
故答案为:①、③、⑤.
点评 本题主要考查矩形的角是直角的性质和勾股定理的运用,要根据三角形的腰长的不确定分情况讨论.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12.以下列长度(单位:厘米)为边的三角形是直角三角形的是( )
| A. | 2,2,3 | B. | 2,3,4 | C. | 3,4,5 | D. | 4,5,6 |
19.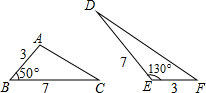 如图,若△ABC和△DEF的面积分别为S1,S2,则( )
如图,若△ABC和△DEF的面积分别为S1,S2,则( )
 如图,若△ABC和△DEF的面积分别为S1,S2,则( )
如图,若△ABC和△DEF的面积分别为S1,S2,则( )| A. | S1=$\frac{1}{2}$S2 | B. | S1=$\frac{7}{2}$S2 | C. | S1=$\frac{8}{5}$S2 | D. | S1=S2 |
16.和温带大陆性气候相比较,温带海洋性气候地区每天气温变化的幅度比较小,较适合人类居住,所以温带海洋性气候地区每天气温的( )比较小.
| A. | 极差 | B. | 平均数 | C. | 众数 | D. | 中位数 |