题目内容
12.定义一种对正整数n的“F运算”:①当n为奇数时,结果为3n+5;②当n为偶数时,结果为$\frac{n}{2^k}$(其中k是使$\frac{n}{2^k}$为奇数的正整数),并且运算重复进行.例如,取n=26,则:
若n=420,则第2015次“F运算”的结果是5.
分析 由n=420是偶数,所以第一次利用②进行计算,得到结果105成为奇数,然后再利用①计算得到结果是320,接着利用②除以64才能成为奇数,结果为5,再利用①结果为20,利用②进行计算除以4,得出结果5就出现循环,利用这个规律即可求出结果.
解答 解:第一次:$\frac{420}{{2}^{2}}$=105,
第二次:105×3+5=320,
第三次:$\frac{320}{{2}^{6}}$=5,
第四次:3×5+5=20,
第五次:$\frac{20}{{2}^{2}}$=5,
第六次:5×3+5=20,
…
∵(2015-2)÷2=1006…1,
∴第2015次运算结果是5.
故答案为:5.
点评 此题考查数字的变化规律,找出数字之间的运算规律,利用规律即可求出结果.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
2.正六边形的每个内角度数是( )
| A. | 60° | B. | 90° | C. | 108° | D. | 120° |
7.如图是一个简单的数值运算程序,当输入的x的值为-1时,则输出的值为( )


| A. | 1 | B. | -5 | C. | -1 | D. | 5 |
2.在Rt△ABC中,∠C=90°,AB=c,AC=b,BC=a,则下列关系中不成立的是( )
| A. | b=c•cosA | B. | a=b•tanB | C. | c=$\frac{a}{cosB}$ | D. | tanA•tanB=1 |
 如图,圆上有五个点,这五个点将圆分成五等份(每一份称为一段弧长),把这五个点按顺时针方向依次编号为1,2,3,4,5,若从某一点开始,沿圆周顺时针方向行走,点的编号是数字几,就走几段弧长,则称这种走法为一次“移位”.如:小明在编号为3的点,那么他应走3段弧长,即从3→4→5→1为第一次“移位”,这时他到达编号为1的点,然后从1→2为第二次“移位”.小明从编号为4的点开始,第三次“移位”后,他到达编号为2的点,第2002次“移位”后,他到达编号为1的点.
如图,圆上有五个点,这五个点将圆分成五等份(每一份称为一段弧长),把这五个点按顺时针方向依次编号为1,2,3,4,5,若从某一点开始,沿圆周顺时针方向行走,点的编号是数字几,就走几段弧长,则称这种走法为一次“移位”.如:小明在编号为3的点,那么他应走3段弧长,即从3→4→5→1为第一次“移位”,这时他到达编号为1的点,然后从1→2为第二次“移位”.小明从编号为4的点开始,第三次“移位”后,他到达编号为2的点,第2002次“移位”后,他到达编号为1的点. 如图,在△ABC中,AB=AC,AC的垂直平分线分别交AB、AC于点D、E.∠DCA=40°,
如图,在△ABC中,AB=AC,AC的垂直平分线分别交AB、AC于点D、E.∠DCA=40°, 已知直角△ABC中,I为△ABC各内角平分线的交点,过I点作BC的垂线,垂足为H,若BC=6,AC=8,AB=10,那么IH的值为2.
已知直角△ABC中,I为△ABC各内角平分线的交点,过I点作BC的垂线,垂足为H,若BC=6,AC=8,AB=10,那么IH的值为2.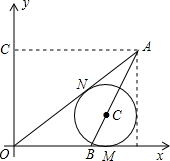 如图,在直角坐标系中,点A的坐标是(8,6),点B的坐标是(5,0),点C在AB上,以C为圆心的圆与x轴相切,与AD切于点N,求⊙C的面积.
如图,在直角坐标系中,点A的坐标是(8,6),点B的坐标是(5,0),点C在AB上,以C为圆心的圆与x轴相切,与AD切于点N,求⊙C的面积.